Entanglement and the Geometry of Spacetime

In 1935, Albert Einstein and collaborators wrote two papers at the Institute for Advanced Study. One was on quantum mechanics [1] and the other was on black holes [2]. The paper on quantum mechanics is very famous and influential. It pointed out a feature of quantum mechanics that deeply troubled Einstein. The paper on black holes pointed out an interesting aspect of a black hole solution with no matter, where the solution looks like a wormhole connecting regions of spacetime that are far away. Though these papers seemed to be on two completely disconnected subjects, recent research has suggested that they are closely connected.

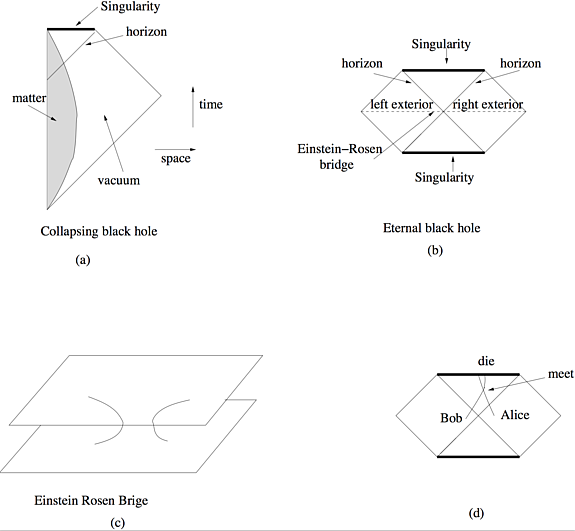
Einstein’s theory of general relativity tells us that spacetime is dynamical. Spacetime is similar to a rubber sheet that can be deformed by the presence of matter. A very drastic deformation of spacetime is the formation of a black hole. When there is a large amount of matter concentrated in a small enough region of space, this can collapse in an irreversible fashion. For example, if we filled a sphere the size of the solar system with air, it would collapse into a black hole. When a black hole forms, we can define an imaginary surface called “the horizon”; it separates the region of spacetime that can send signals to the exterior from the region that cannot. If an astronaut crosses the horizon, she can never come back out. She does not feel anything special as she crosses the horizon. However, once she crosses, she will be inevitably crushed by the force of gravity into a region called “the singularity” (Figure 1a).

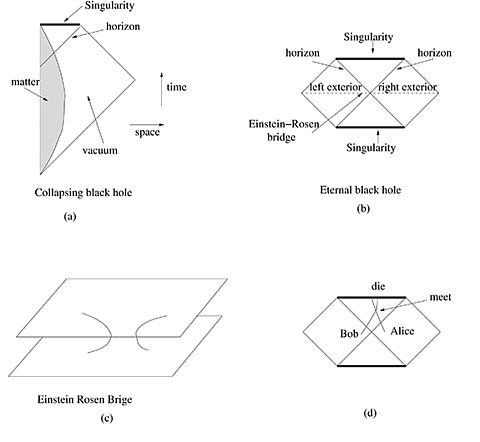
Outside of the distribution of collapsing matter, black holes are described by a spacetime solution found by Karl Schwarzschild in 1916. This solution turned out to be very confusing, and a full understanding of its classical aspects had to wait until the 1960s. The original Schwarzschild solution contained no matter (Figure 1b). It is just vacuum everywhere, but it has both future and past singularities. In 1935, Einstein and Nathan Rosen found a curious aspect of this solution: it contains two regions that look like the outside of a black hole. Namely, one starts with a spacetime that is flat at a far distance. As we approach the central region, spacetime is deformed with the same deformation that is generated outside a massive object. At a fixed time, the geometry of space is such that as we move in toward the center, instead of finding a massive object, we find a second asymptotic region (Figure 1c). The geometry of space looks like a wormhole connecting two asymptotically flat regions. This is sometimes called the Einstein–Rosen bridge. They realized this before the full geometry was properly understood. Their motivation was to find a model for elementary particles where particles were represented by smooth geometries. We now think that their original motivation was misguided. This geometry can also be interpreted as a kind of wormhole that connects two distant regions in the same spacetime. John Wheeler and Robert Fuller showed that these wormholes are not traversable, meaning it is not possible to physically travel from one side of the wormhole to the other. [3] We can think of this configuration as a pair of distant black holes. Each black hole has its own horizon. But it is a very particular pair since they are connected through the horizon. The distance from one horizon to the other through the wormhole is zero at one instant of time. Let us consider two observers, Alice and Bob, outside each of the black holes. For a brief moment in time, the horizons of the two black holes touch, then they move away from each other. Alice cannot send a signal to Bob if she stays outside the horizon of her black hole. However, Alice and Bob could both jump into their respective black holes and meet inside. It would be a fatal meeting since they would then die at the singularity. This is a fatal attraction.

Wormholes usually appear in science fiction books or movies as devices that allow us to travel faster than light between very distant points. These are different than the wormhole discussed above. In fact, these science fiction wormholes would require a type of matter with negative energy, which does not appear to be possible in consistent physical theories.

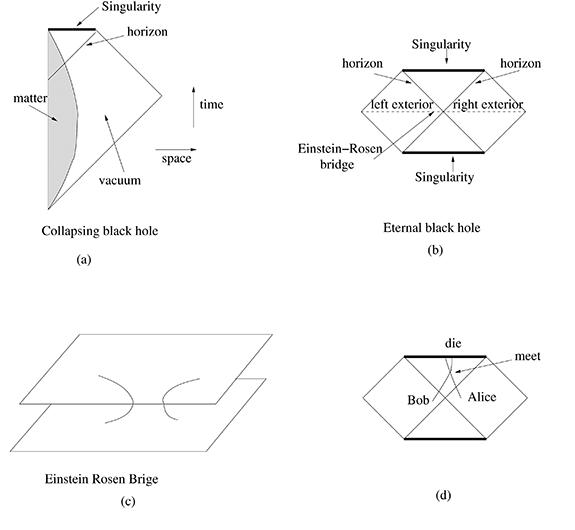
In black holes that form from collapse, only a part of the Schwarzschild geometry is present, since the presence of matter changes the solution. This case is fairly well understood and there is no wormhole. However, one can still ask about the physical interpretation of the solution with the two asymptotic regions. It is, after all, the general spherically symmetric vacuum solution of general relativity. Surprisingly, the interpretation of this solution involves the paper by Einstein, Boris Podolsky, and Rosen (EPR) written in 1935 [1]. By the way, the EPR paper shows that Einstein really did very influential work after he came to the IAS.

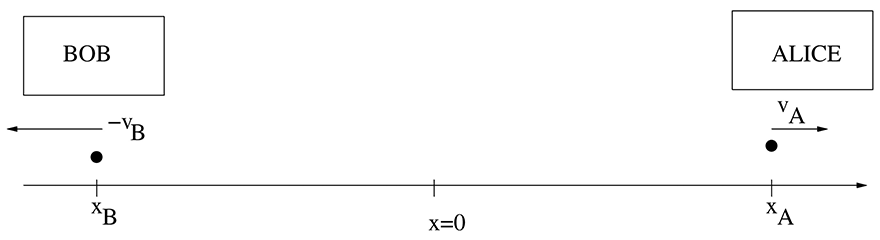
The EPR paper pointed out that quantum mechanics had a very funny property later called “quantum entanglement,” or, in short, “entanglement.” Entanglement is a kind of correlation between two distant physical systems. Of course, correlations between distant systems can exist in classical systems. For example, if I have one glove in my jacket and one in my house, then if one is a left glove, the other will be a right glove. However, entanglement involves correlations between quantum variables. Quantum variables are properties that cannot be known at the same time; they are subject to the Heisenberg uncertainty principle. For example, we cannot know both the position and the velocity of a particle with great precision. If we measure the position very precisely, then the velocity becomes uncertain. Now, the idea in the EPR paper is that we have two distant systems; in each distant system, we can measure two variables that are subject to the uncertainty principle. However, the total state could be such that the results of distant measurements are always perfectly correlated, when they both measure the same variable. The EPR example was the following (Figure 2). Consider a pair of equal-mass particles with a well-defined center of mass, say x = 0, and also with a well-defined relative velocity, say v_rel = v_A − v_B. First, a small clarification. The Heisenberg uncertainty principle says that the position and the velocity cannot be known at the same time. When we have two independent dynamical variables—two independent positions and two independent velocities—then it is possible to know the position of one and the velocity of the other. Since the center of mass and relative position are independent variables, then it is indeed possible to start with the state that EPR postulated. Now for the more surprising part: let us say that two distant observers, call them Alice and Bob, both measure the positions of the respective particles. They find that if Alice measures some value x_A, then Bob should measure x_B = −x_A. On the other hand, if Alice measures the velocity v_A, then we know that Bob should measure the definite velocity v_B = v_A − v_rel. Of course, Alice and Bob should each make a choice of whether they want to measure the velocity or the position. If Alice measures the position and Bob the velocity, they find uncorrelated results. Note that when Alice decides to measure the position, Bob’s particle, which could be very distant, seems to “decide” to have a well-defined position also. On the other hand, when Alice measures the velocity, Bob’s particle “decides” to have a well-defined velocity. At first sight, this would seem to allow instantaneous communication between Alice and Bob. It would seem that Alice can encode a message of zeros and ones by deciding to measure either her particle’s position or velocity and then all that Bob has to do is to see whether his particle has well-defined position or velocity. However, it is possible to show that Bob cannot “read” such a message. These correlations do not allow us to send signals faster than light.

Entanglement appears to be a very esoteric property of quantum mechanical systems. But in the past twenty years, people have found many practical uses for these correlations. Among them is the possibility of Alice and Bob communicating secretly while making sure that the NSA (National Security Agency) is not eavesdropping on the communication.

Let us now return to black holes. There is an important feature of black holes that arises when one considers them as quantum mechanical objects. In 1974, Stephen Hawking argued that quantum mechanics implies that black holes have a temperature, with smaller black holes having a higher temperature. A small enough black hole can be red-hot. In fact, one can even have a white black hole! This is a theoretical prediction that has not yet been verified experimentally because the black holes that are naturally produced by the collapse of stars are too cold for this radiation to be measurable. This thermal property of black holes has an important consequence. As we have known since the nineteenth century, temperature is due to the motion of a large number of microscopic constituents of the system. Thus, black holes should have microscopic constituents that can be in a large number of possible quantum mechanical configurations or “microstates.” In fact, we think that black holes, as seen from the outside, behave as ordinary quantum mechanical systems.

One can consider, therefore, a pair of black holes where all the microstates are “entangled.” Namely, if we observe one of the black holes in one particular microstate, then the other has to be in exactly the same microstate. A pair of black holes in this particular EPR entangled state would develop a wormhole, or Einstein-Rosen bridge, connecting them through the inside. The geometry of this wormhole is given by the fully extended Schwarzschild geometry. It is interesting that both wormholes and entanglement naively appear to lead to a propagation of signals faster than light. But in either case this is not true, for different detailed reasons. The net result is the same: we cannot use either of them to send signals faster than light. This picture was developed through the years starting with work by Werner Israel [4]. Most recently, Leonard Susskind and I emphasized this ER=EPR connection as a way to resolve some apparent paradoxes regarding the black hole interior [5, 6].

There are several interesting lessons regarding this picture of geometry emerging from entanglement. Perhaps the deepest one is that the peculiar and strange property of quantum mechanical entanglement is behind the beautiful continuity of spacetime. In other words, the solid and reliable structure of spacetime is due to the ghostly features of entanglement. As we entangle two systems with many degrees of freedom, it seems possible to generate a geometric connection between them, even though there is no direct interaction between the two systems. 

Recommended Reading: Dennis Overbye writes about the latest debates involving the quantum mechanical property of entanglement—originating with the EPR paper and arriving at Juan Maldacena’s most recent findings with Leonard Susskind—in a recent New York Times article, “A Black Hole Mystery Wrapped in a Firewall Paradox”; visit http://ow.ly/nWftw/.