In a paper written in 1939, Albert Einstein attempted to reject the notion of black holes that his theory of general relativity and gravity, published more than two decades earlier, seemed to predict. “The essential result of this investigation,” claimed Einstein, who at the time was six years into his appointment as a Professor at the Institute, “is a clear understanding as to why the ‘Schwarzschild singularities’ do not exist in physical reality.”
Schwarzschild singularities, later coined “black holes” by John Wheeler, former Member in the School of Mathematics, describe objects that are so massive and compact that time disappears and space becomes infinite. The same year that Einstein sought to discount the existence of black holes, J. Robert Oppenheimer, who would become Director of the Institute in 1947, and his student Hartland S. Snyder used Einstein’s theory of general relativity to show how black holes could form. The above photo, taken at the Institute in the late 1940s, shows Oppenheimer with Einstein. According to Jeremy Bernstein, a physicist, author, and former Member in the School of Mathematics, it is unknown whether Einstein and Oppenheimer ever discussed black holes, but neither worked on the subject again.
Below, Juan Maldacena, Professor in the School of Natural Sciences, explains the development of a string theoretic interpretation of black holes where quantum mechanics and general relativity, theories previously considered incompatible, are united. Work by Maldacena and others has given a precise description of a black hole, which is described holographically in terms of a theory living on the horizon. According to this theory, black holes behave like ordinary quantum mechanical objects—information about them is not lost, as previously thought, but retained on their horizons—leading physicists to look at black holes as laboratories for describing the quantum mechanics of spacetime and for modeling strongly interacting quantum systems.
The ancients thought that space and time were preexisting entities on which motion happens. Of course, this is also our naive intuition. According to Einstein’s theory of general relativity, we know that this is not true. Space and time are dynamical objects whose shape is modified by the bodies that move in it. The ordinary force of gravity is due to this deformation of spacetime. Spacetime is a physical entity that affects the motion of particles and, in turn, is affected by the motion of the same particles. For example, the Earth deforms spacetime in such a way that clocks at different altitudes run at different rates. For the Earth, this is a very small (but measurable) effect. For a very massive and very compact object the deformation (or warping) of spacetime can have a big effect. For example, on the surface of a neutron star a clock runs slower, at 70 percent of the speed of a clock far away.
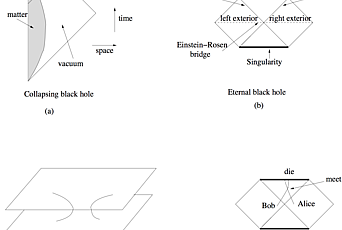
In fact, you can have an object that is so massive that time comes to a complete standstill. These are black holes. General relativity predicts that an object that is very massive and sufficiently compact will collapse into a black hole. A black hole is such a surprising prediction of general relativity that it took many years to be properly recognized as a prediction. Einstein himself thought it was not a true prediction, but a mathematical oversimplification. We now know that they are clear predictions of the theory. Furthermore, there are some objects in the sky that are probably black holes.
Black holes are big holes in spacetime. They have a surface that is called a “horizon.” It is a surface that marks a point of no return. A person who crosses it will never be able to come back out. However, he will not feel anything special when he crosses the horizon. Only a while later will he feel very uncomfortable when he is crushed into a “singularity,” a region with very high gravitational fields. The horizon is what makes black holes “black”; nothing can escape from the horizon, not even light. Fortunately, if you stay outside the horizon, nothing bad happens to you. The singularity remains hidden behind the horizon.
Something surprising happens when we take into account the effects of quantum mechanics. Due to quantum mechanical fluctuations near the horizon, black holes should emit radiation, called Hawking radiation.This is a famous theoretical prediction that Stephen Hawking made in the seventies. This means that black holes are not completely black. A black hole can glow, like an ember, or, if it is hot enough, you can even have the oxymoronic possibility of a white black hole. A black hole gets hotter the smaller it is. A white black hole should have the size of a bacterium, and the mass of a continent. Such black holes, while theoretically possible, are not known to be naturally produced anywhere in the universe. Black holes that are naturally produced have masses bigger than the Sun and sizes bigger than a few miles. Such black holes are also supposed to emit Hawking radiation, but it is swamped by other matter falling into the black hole. For this reason, Hawking radiation has not been directly measured. However, the argument leading to it is so solid that most scientists who have studied it think it is a very clear prediction. The existence of this radiation has important consequences.The first is that black holes have a temperature. We know that temperature is due to the motion of the elementary constituents of the object. For example, air is hotter or colder depending on whether air molecules are moving faster or slower. In the case of black holes, what is moving? Black holes only involve gravity, so what is moving is spacetime itself. Since the nineteenth century, we have understood that when we have thermal systems we can compute a quantity called the “entropy,” which tells us about the number of microscopic configurations that the system has. From Hawking’s formula for the temperature of a black hole one can also find this entropy. It turns out to be proportional to the area of the horizon, or the square of the mass of the black hole. This is also a bit strange. The entropy of almost every substance grows in proportion to the amount of substance that we have. Here it grows like the square. It is really a case of “the more the merrier.”
A second consequence of Hawking radiation is that black holes lose mass, since they are radiating energy away. Thus, a black hole left alone in an otherwise empty universe would eventually completely disappear. We call this process “black hole evaporation,” since the black hole appears to evaporate as a droplet of water.
Hawking radiation from black holes has given rise to very profound and interesting theoretical puzzles. Einstein has taught us that spacetime is a physical object. We also know that all other physical objects, such as those made with matter or radiation, obey the laws of quantum mechanics. Thus, spacetime should be no different and should also obey the laws of quantum mechanics. Any quantum mechanical theory of spacetime should be able to describe precisely how black holes form and evaporate. It should also give a precise explanation for the entropy of a black hole.
Here one finds an interesting paradox. Classically, all the information making the black hole has fallen inside. On the other hand, Hawking radiation implies that the black hole emits thermal radiation. This thermal radiation apparently carries no information about the things that fell in, since this radiation is generated in the vicinity of the horizon. Thus the black hole can form in many different ways but it appears to evaporate always in the same way. This is a contradiction with standard quantum mechanics. In quantum mechanics (as in classical mechanics) the information about a system is not lost. Different initial conditions lead to different outcomes. It can be the case that sometimes the outcomes are very similar. For example, if one puts this article in a shredder, one seems to lose what was written on it. However, one could, in principle, put it back together. Hawking suggested that black holes imply that this basic principle of quantum mechanics would not hold in the presence of gravity. Namely, the radiation coming out of black holes would be completely thermal and devoid of the information of what fell into black holes. Thus, black holes appear to be sinks of information, perverse monsters that threaten the fundamental laws of quantum mechanics.
String theory is a theory being constructed to describe the quantum mechanics of spacetime. As such, the theory should explain whether black holes are consistent with quantum mechanics or not. In fact, since string theory obeys the usual principles of quantum mechanics, we expect that information should not be lost in black holes. For this reason the problem of information loss was actively studied during the nineties. The problem was difficult in the original formulation of string theory because the quantum spacetime was described by starting with a flat spacetime and then considering small quantum fluctuations, or ripples, that propagate in it. As long as these ripples interact weakly with each other, the theory is relatively simple. However, in order to form a black hole you need a strong deviation from a flat spacetime. You need to put a lot of these ripples together, and by the time the black hole forms, the simplest formulation of string theory becomes unmanageable.
In the mid-nineties, Joseph Polchinski (at the University of California, Santa Barbara) made a breakthrough by discovering that string theory contains other objects, called D-branes. They have a strange name for reasons that are not important for us. You can mentally give them any other name that you find more pleasant. These are particle-like objects that are heavier than the spacetime ripples we discussed above. Nevertheless, one can give a very precise description for them within the rules of string theory. It soon became clear that they were ideally suited for studying black holes.
The description of a single D-brane is fairly simple. A single D-brane is very similar to a particle; it is characterized by its position in space. However, a single D-brane is not heavy enough to curve spacetime in a significant way. So, we need to bring many D-branes together. When we bring them together, there is a surprising new symmetry that emerges. In ordinary quantum mechanics, elementary particles are identical, in the sense that there is no way to distinguish them. The full description is completely invariant under the interchange of any two identical elementary particles, such as two electrons. D-branes are invariant under a bigger symmetry group: a full continuous symmetry, called a gauge symmetry. (For the mathematically oriented: this is the group SU(N) versus the permutation group SN). When N D-branes come together, the positions of the branes become N x N matrices. A matrix is an array of numbers. We would have expected that N branes are described by N positions, the positions of each of the objects individually. However, we find that they are described by N2 numbers. The dynamics of these N2 variables is governed by a gauge theory. Gauge theories are very important for the description of nature; we use them to describe three of the forces (the electromagnetic, the weak, and the strong). Now, if we want to separate the D-branes by a big amount, we find that there is a force that does not allow them to be separated unless the matrices are diagonal, reducing then to the usual description in terms of N identical particles. When all these D-branes are close together, the number of possible ways to arrange them grows very fast with its number. It grows like N2, rather than the N expected for a usual extensive system.
This has become a bit abstract, so let us make an analogy. Say D-branes are people. Imagine that we have a group of N people (say N is a big number, e.g., a thousand). Now imagine that each person can be happy or sad. The entropy is just the information that you need to completely specify the emotional state of everybody. In this case you need to specify N bits of information: whether each of the N persons is happy or sad. If N is a thousand, you need a kilobit of information. On the other hand, imagine that each person can like or dislike every other person. Now to capture the complete set of likes or dislikes of everybody you need to give N2 bits of information. If N is a thousand, you need a megabit of information. The case of black holes is similar to this latter situation, where one has to keep track of variables that involve pairs of D-branes, rather than single D-branes. In this analogy, you can only separate the D-branes when they dislike (and are disliked by) all the other D-branes, so the number of configurations becomes much smaller.
A large number of D-branes is heavy enough to warp the spacetime around them and to produce a black hole. In order to produce a black hole with some temperature it is necessary to excite these N2 degrees of freedom. This leads to a precise microscopic accounting for the entropy of the black holes, as shown by Andrew Strominger and Cumrun Vafa (both former Members of IAS). These N2 degrees of freedom produce a highly entangled state that cannot be described in terms of the motion of the individual particles. However, it can be described very precisely in terms of the gauge theory of the N x N matrices. This gauge theory is not particularly different from the ones we use to describe the strong force in nature. Some details are different. However, in some very important respects it is the same. First, it obeys the usual rules of quantum mechanics. Second, it lives on a fixed spacetime—in this case, the point in spacetime where the branes are sitting.
Actually, this leads us into an apparent contradiction. On the one hand, we said that we can describe the branes in terms of a gauge theory living at a spatial point. On the other hand, we said that the branes form a black hole, which has a non-zero horizon size.
In fact, in string theory, these two descriptions are viewed as equivalent. The gauge theory is describing the whole region around the black hole. If we view the black hole from very far away, it looks like a point—that is why the matrices live at a point. On the other hand, the matrices also give rise to the whole spacetime region around the horizon of the black hole. This is the gauge/gravity correspondence proposed by myself and Edward Witten (at IAS) and Steven Gubser, Igor Klebanov, and Alexander Polyakov (at Princeton University).
The gauge theory gives a precise description of the black hole and its surrounding geometry. It is described in terms of a perfectly ordinary quantum mechanical system. This explains its entropy. It also gives a completely quantum mechanical description of the black hole and the spacetime around the black hole. This description is sometimes called “holographic” because the whole spacetime emerges dynamically from a quantum mechanical description that lives in a smaller number of dimensions. (An ordinary hologram is a two-dimensional surface that produces a three-dimensional image when it is illuminated.)
Going back to the analogy of the group of people and the pattern of likes and dislikes, the idea is that the whole spacetime is encoded in the pattern of likes and dislikes among the various people. A spacetime ripple is a change in that pattern. The “gauge theory” is a simple dynamical law that says how this pattern changes.
This description has been explored actively here at the Institute and elsewhere. It is best understood in very special configurations in string theory. However, similar descriptions are expected to be valid for black holes in general. These theoretical developments were made with the goal of showing that black holes behave like ordinary quantum mechanical objects. More recently, the same relation is being explored in order to model strongly interacting quantum systems via black holes. Thus, in some sense, black holes have become a source of information, rather than the sinks they were feared to be!
Recommended reading: The Black Hole War by Leonard Susskind (Little, Brown and Company, 2008)