Robert P. Langlands Awarded 2018 Abel Prize

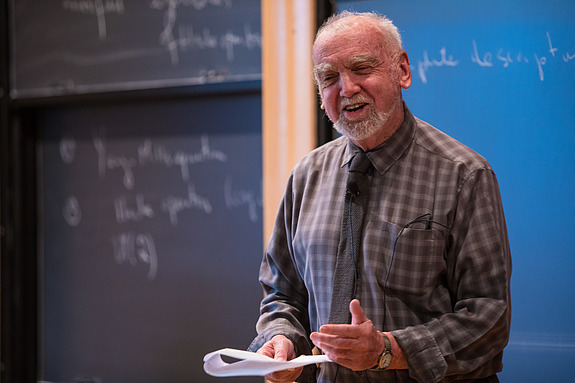
The Norwegian Academy of Science and Letters has awarded the 2018 Abel Prize to Robert P. Langlands, Professor Emeritus in the School of Mathematics at the Institute for Advanced Study. Langlands was cited by the Abel Committee “for his visionary program connecting representation theory to number theory.”

A set of overarching and interconnected conjectures collectively known as the Langlands program has had a deep influence across a broad sweep of mathematics and parts of theoretical physics. The origins of the program are found in a seventeen-page handwritten letter that Langlands wrote in 1967 to André Weil, a Professor at the Institute at the time, in which he proposed a grand unifying theory that relates seemingly unrelated concepts in number theory, algebraic geometry, and the theory of automorphic forms. A typed copy of the letter, made at Weil’s request for easier reading, circulated widely among mathematicians in the late 1960s and 1970s, and for more than four decades, mathematicians have been working on its conjectures.

“The Institute is incredibly proud and pleased that Robert Langlands has received the great honor of the 2018 Abel Prize in recognition of his visionary program,” said Robbert Dijkgraaf, Director and Leon Levy Professor. “Bob’s deep insights have inspired generations of mathematicians and yielded many profound breakthroughs. The course he charted will guide the future of mathematics and will undoubtedly lead to new surprising discoveries—a gift to the world, that keeps on giving.”

Peter Sarnak, Professor in the Institute’s School of Mathematics, added, “The Langlands program and its core conjecture (functoriality) were born out of concrete and far-reaching breakthroughs that Langlands achieved early on. Once he recognized these unifying themes, Langlands (and his students and his “school”) spent much of his time and effort developing fundamental tools (such as the trace formula) in order to establish many cases of his conjectures. These cases are all hard earned and have often proven to be the basis for spectacular works by others (a well-known example is Langlands’s base change theorem, which was the starting point of Wiles’s proof of Fermat’s last theorem).”

The Abel Prize is an international award that acknowledges outstanding scientific work in the field of mathematics and comes with a monetary award of nearly $800,000. The Prize will be given to Langlands by H.M. King Harald V at an award ceremony in Oslo on May 22. Since the Abel Prize was first bestowed in 2003, 17 of the 19 recipients have been affiliated with the Institute as Faculty or Members.

Langlands’s profound insights in number theory and representation theory include the formulation of general principles relating automorphic forms and algebraic number theory; the introduction of a general class of L-functions; the construction of a general theory of Eisenstein series; the introduction of techniques for dealing with particular cases of the Artin conjecture (that proved to be of use in the proof of Fermat’s last theorem); the introduction of endoscopy; and the development of techniques for relating the zeta functions of Shimura varieties to automorphic L-functions.

Born in British Columbia in 1936, Langlands grew up in a small Canadian town where his father owned a building supply store. He enrolled at the University of British Columbia at age 16, where he was drawn to mathematics over physics, particularly algebraic computations. After earning his bachelor’s and master’s degrees from the University of British Columbia, Langlands earned his Ph.D. from Yale University in 1960. He taught at Princeton University and Yale University, became a Member in the Institute’s School of Mathematics in 1962, and was appointed to the Faculty of the Institute in 1972.

In his conjectures, Langlands drew on the work of Harish-Chandra, Atle Selberg, Goro Shimura, André Weil, and Hermann Weyl, among others with extensive ties to the Institute. His early work in representation theory involved adapting the methods of former IAS Professor Harish-Chandra to the theory of automorphic forms. “His papers were among the first— Selberg’s papers and then Harish-Chandra’s—that I studied very carefully, that I actually worked with, that I actually used in what I was doing,” Langlands has said.

Endoscopy, which aims to distinguish the internal structure of automorphic representations of different groups, arose from Langlands’s study of the zeta functions of Shimura varieties developed by former IAS Member Goro Shimura and in the theory of the discrete series, a theory created by Harish-Chandra at the Institute in the sixties. The modern theory of Shimura varieties, so named by Langlands in the 1970s, began with the development of the theory of abelian varieties with complex multiplication by Shimura, Yutaka Taniyama, and Weil in the mid-1950s.

Langlands’s principle of functoriality, which in the many cases where it has been proved uses the Selberg trace formula and the fundamental lemma to link automorphic representations of different groups through their L-groups, was informed by the theory of class fields, and the representation theory of semisimple Lie groups in the form given to it by Harish-Chandra.

Some aspects of the Langlands program have been proven, such as Laurent Lafforgue’s proof of the “Langlands conjecture for function fields,” which Lafforgue presented in a series of lectures at the Institute in 1999 and for which he won a Fields Medal in 2002. While a Member at the Institute, Bao Châu Ngô realized a proof of the fundamental lemma, a technical device formulated by Langlands that links automorphic representations of different groups, for which Ngô was awarded a Fields Medal in 2010. Other aspects have led to proofs of seemingly unrelated theorems, such as Andrew Wiles’s 1994 proof of Fermat’s last theorem.

Much of the modern theory of automorphic forms is governed by two fundamental problems that are at the heart of the Langlands program: Langlands’s principle of functoriality and the general analogue of the Shimura-Taniyama-Weil conjecture on modular elliptic curves. The work of Wiles that led to the proof of Fermat’s last theorem suggests that the two problems, among the deepest questions in mathematics, are inextricably linked.

In addition to changing the field of automorphic forms drastically, making the infinite-dimensional representation theory of reductive groups into a major field of mathematical activity, and introducing a general class of L-functions that have had major consequences for algebraic number theory, Langlands’s conjectures have had a significant influence on other fields, such as physics. In the geometric Langlands program, created by former IAS Member Vladimir Drinfeld and collaborators, some of the ideas are converted from number theory into statements in geometry. The geometric form is particularly rich for implications in theoretical physics, especially string theory. In 2006, Edward Witten, Charles Simonyi Professor in the School of Natural Sciences, cowrote a 225-page paper on the relation of part of the geometric Langlands program to ideas of the duality between electricity and magnetism.

Among Langlands’s honors are the Shaw Prize in Mathematical Sciences (2007); the Frederic Esser Nemmers Prize in Mathematics (2006); the Grande Médaille d’Or (Gold Medal) of the French Academy of Sciences (2000); the Wolf Prize in Mathematics (jointly with Andrew Wiles, 1996); the inaugural National Academy of Sciences Award in Mathematics (1988); the Common Wealth Award (1984); and the American Mathematical Society’s Cole Prize (1982).

About the Norwegian Academy of Science and Letters
The Norwegian Academy of Science and Letters was founded in 1857. It is a nongovernmental, nationwide body that embraces all fields of science and scholarship. The Academy has Norwegian and foreign members, as well as honorary members. The members are divided into two sections: Mathematics and Natural Sciences, and Humanities and Social Sciences. In addition to the Abel Prize, the Academy awards the Kavli Prize in astrophysics, nanoscience, and neuroscience.

About the Institute for Advanced Study
The Institute for Advanced Study is one of the world’s leading centers for theoretical research and intellectual inquiry. The Institute exists to encourage and support curiosity-driven research in the sciences and humanities—the original, often speculative thinking that produces advances in knowledge that change the way we understand the world. Work at the Institute takes place in four Schools: Historical Studies, Mathematics, Natural Sciences, and Social Science. It provides for the mentoring of scholars by a permanent Faculty, and it ensures the freedom to undertake research that will make significant contributions in any of the broad range of fields in the sciences and humanities studied at the Institute.

The Institute, founded in 1930, is a private, independent academic institution located in Princeton, New Jersey. Its more than 8,000 former Members have held positions of intellectual and scientific leadership throughout the academic world. Thirty-three Nobel Laureates and 41 out of 56 Fields Medalists, as well as many winners of the Wolf and MacArthur prizes, have been affiliated with the Institute.