Black Holes, Quantum Information, and the Structure of Spacetime

In the last six months, Juan Maldacena, Carl P. Feinberg Professor in the School of Natural Sciences, has received three major awards: the Lorentz Medal of the Royal Netherlands Academy of Arts and Sciences; the 2018 Einstein Medal from the Albert Einstein Society in Bern; and most recently the Richard E. Prange Prize and Lectureship in Condensed Matter Theory and Related Areas.
The awards have recognized his groundbreaking contribution to the understanding of the quantum physics of black holes. Maldacena conjectured in 1997 a deep connection between gauge theories, which describe the world of particle physics at the microscopic scale, and quantum gravity, which describes the physics of gravitational forces of the universe. Known as the anti-de Sitter/conformal field theory (AdS/CFT) correspondence, or gauge/gravity duality, it is one of the most actively studied topics in theoretical physics with more than 10,000 citations, making it among the most-cited papers in science over the last two decades.
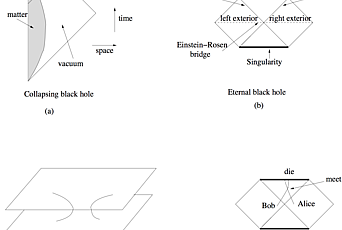
More recently, Maldacena and Leonard Susskind proposed in 2013 that certain black hole paradoxes, related to the Hawking information paradox, could be resolved if outgoing particles and the black hole are connected by wormholes. Often referred to as "ER=EPR," the paper connects two works that Einstein authored at the Institute in 1935. "ER" refers to a paper written by Einstein and Nathan Rosen (an IAS Member at the time) that suggests that black holes could come in pairs connected by Einstein-Rosen bridges, or wormholes. "EPR" refers to a paper written by Einstein, Boris Podolsky (also a Member at the time), and Rosen, which points out the quantum mechanical property of entanglement. Maldacena and Susskind's concept proposes that entanglement and wormholes create spacetime, which emerges from connected bits of quantum information. The following is an edited Q&A with the Institute Letter.
IL: First of all, congratulations on your recent awards. Obviously, your research has been recognized for some time (a MacArthur Fellowship in 1999, the Dirac Prize and Medal in 2007, the Fundamental Physics Prize in 2012, among many others), but is there a reason we are seeing so much recognition of your work at this particular moment?
JM: Oh, I don't know [laughter]. In condensed matter physics and in several other areas of physics, one is interested in understanding the behavior of particles that are strongly interacting and described by quantum mechanics. Quantum theory is easy to analyze when the particles are almost free, but when the particles are strongly interacting, it is difficult—there could be all kinds of different surprising behavior. The AdS/CFT correspondence or gauge/gravity duality relates certain very strongly interacting systems to a theory of gravity. In this way, it converts a problem that is difficult on the quantum mechanical side to a problem that is relatively simpler on the gravity side.
IL: When you say condensed matter physics, what types of materials are we talking about that are applicable?
JM: One problem, for example, that people are interested in is high-temperature superconductivity. But there could be some new materials people are trying to design that have strong interactions. And also, with the possible advent of quantum computers, these materials would be able to be designed more or less at will.
Where the theory could help in high-temperature superconductivity is in understanding the phenomenon better, and maybe finding new instances of the phenomenon, or finding even some behaviors that we don't know now that are possible.
An example of a relationship between the two is what Douglas Stanford has studied. He found a connection between quantum chaos and the physics of black holes and the physics near the horizons of black holes.
IL: And when we are talking about black holes, we aren't talking about the black holes that cosmologists study...
JM: That's right. These are black holes that exist in other auxiliary universes, which are very small, relatively small. The interesting thing is that these very strongly interacting systems can behave as if they are creating their own universe. It is a theory of a universe in a bottle.
IL: And by very small, can you provide some context?
JM: The problem is that it is difficult to define the scale, because it could mean different things. They are small in the sense that they exist in a lab, but they are also small in the sense that, in the theory of gravity, there is a fundamental distance scale where the classical description of spacetime breaks down due to quantum mechanical effects. The idea is that the overall size of the universe, in units of this distance, is also relatively small. Our universe is very big compared to this fundamental distance, which is 10-33 cm. This is a distance that is very, very small, while the overall size of the universe is much bigger than that.
IL: When you say that these are in a lab, do they actually exist in a lab, or is it a theoretical lab?
JM: It is a theoretical lab, for now. They could somehow exist in a lab, in the future, when quantum computers are a little better than they are today or people find more ingenious ways to create them.
IL: Are these theories for black holes in a theoretical lab connected to real black holes? Are they in theory the same?
JM: They are the same in the sense that they are governed by the same equations, but they are not the same in other details. In a black hole that exists in nature, there are other particles, like electrons and photons, forming the ordinary matter that exists around the astrophysical black holes. This is different than the type of matter that could exist around these other black holes. What they have in common is that both are described by a dynamical spacetime. In both cases, there is a certain spacetime that can be curved. In both cases, there is this notion of having a horizon, and in both cases, there is a Hawking radiation. The Hawking radiation is not very important for very big astrophysical black holes, for example, where their temperatures are smaller than the temperatures around it. The temperature is not very important. But it is a more important effect for these smaller theoretical black holes.
Recommended Viewing: For more information about black holes, quantum information, and the structure of spacetime, view the public lecture “The Cool Alter-Ego of a Black Hole” by Professor Juan Maldacena and Member Douglas Stanford (recently named by Science News as one of ten “Scientists to Watch,” age 40 or under, who are shaping the science of the future) followed by a panel discussion with IAS Director Robbert Dijkgraaf here. Lectures from PiTP 2018, “From Qubits to Spacetime,” may be viewed here. Some videos from the quantum information and black holes workshop held in December 2017 are available here.
IL: Why are you interested in studying black holes theoretically? What is the burning question?
JM: The reason we are studying these quantum aspects of black holes is to understand the quantum mechanical nature of spacetime. That is not important for astrophysical black holes, but it is very important for the beginning of the Big Bang. Understanding quantum aspects of black holes could be helpful for understanding the beginning of the universe—that is the hope, that is the big-picture, long-term program.
IL: How has thinking about black holes and spacetime changed since you started working in the field?
JM: Black holes were thought to be something that existed somewhere else in the universe and were produced by the four-dimensional gravity that we experience. Now we can associate them to a physical system that does not contain gravity, such as a superconductor or some other system made of subatomic particles. And if these systems are interacting strongly enough, they can generate their own spacetime, and then the black holes can exist.
IL: What does it mean when we hear that spacetime is emergent and not fundamental?
JM: Spacetime being fundamental means that you make the assumption or the hypothesis that it exists, and from there you then construct your theory. Emergent means that it is not something you started from.
IL: When did this idea of emergent spacetime take form? Was it because of the AdS/ CFT correspondence?
JM: There were different indications. But I would say mainly through research in string theory. The gauge/gravity duality was another example of this.
My opinion is that spacetime looks emergent when you start from quantum particle theory, but it could be that there is an alternative description where spacetime is also fundamental, and the two descriptions are just two different ways of describing the same system. That is the idea of duality. It means that the same theory can be described in terms of different building blocks. Another analogy for this is that you could describe a novel, let's say, in English, or you could describe it in French, but it is the same novel.
IL: You wrote about "ER=EPR" and quantum entanglement for the Institute Letter in 2013. What advances have been made since then?
JM: That article was about entanglement and wormholes and I think the main update is a paper by Ping Gao, Daniel Louis Jafferis (School of Natural Sciences Member, 2010–11), and Aron Wall (School of Natural Sciences Member, 2014–17), who realized that there was a way to make this wormhole traversable. The basic idea is that if you have two systems that are very far away—they are not interacting but they are entangled—then you have a wormhole. But if the wormhole is not traversable, that means you cannot travel through the wormhole. If you try to travel through the wormhole, you die. But they realized that if you bring these two systems near each other, and you let them interact a little bit, then you can go through this wormhole.
I recently wrote a paper with Alexey Milekhin and Fedor Popov where we have constructed a solution of the Standard Model, which is the theory of particles in our universe, that has this feature. From the outside, it looks like two black holes, and it has a wormhole connecting them, a traversable wormhole. It would have to be very microscopic, so it is a very tiny thing. It is just a solution of the equations.
IL: So it is not on the scale you would think of in terms of science fiction . . .
JM: No, we would not be able to travel through these wormholes. We would be able to send elementary particles through them. These wormholes are very, very tiny, smaller than the smallest distances we can see today.
IL: Are we talking about quantum information surviving this traversable wormhole?
JM: Well, the theory is that quantum information would survive falling into any black hole, and would be reprocessed, and so on. This process of going through the wormhole is closely connected to something called quantum teleportation, which is something that was discovered in the '80s. It is the ability to transport quantum information via entanglement, and also some classical communication. Quantum teleportation was invented and suggested as a way to make communication secure. It is an unbreakable code because the information goes through a wormhole that cannot be seen from the outside.
IL: What does gravity seem to know about quantum mechanics?
JM: Black holes obey the laws of thermodynamics. And that fact comes from Einstein's equations. Somehow Einstein's equations know about the laws of thermodynamics when you consider a black hole. And this looks very strange, because when Einstein wrote his equations, he wasn't thinking about information or averages, or randomness, or anything like this. These were just classical equations, and the fact that these equations know about thermodynamics is very surprising.
IL: Are you finding that more physics Members are interested in quantum computing?
JM: We have people who are applying some quantum information theory techniques to the study of black holes. We don't have anyone that does quantum computing, per se. But I am a member of a collaboration that has some people doing this, and we have organized workshops where people doing quantum computing come here. Prospects in Theoretical Physics this summer explored connections between quantum computing and black holes. One of the speakers was Scott Aaronson (School of Mathematics Member, 2004–05), who will be involved in a workshop that we will hold in December. We held a similar workshop on black holes and quantum information last year. One of the organizers of this year's workshop is Jonathan Oppenheim who works in quantum information theory.
IL: What does it mean when a black hole is referred to as a quantum computer?
JM: You can think of an ordinary system, even nature, as a kind of machine. And when you have an ordinary machine, it is useful to understand how information is traveling through the machine. It is useful to think of how different parts relate to each other, and how the motion of one relates to the motion of the other.
The detailed dynamical laws tell you how this happens but understanding the flow of information is something basic that constrains how the machine can work. Nature is quantum mechanical, so the machine obeys the laws of quantum mechanics. To understand how information travels around this machine, you have to talk about quantum information. It is information that is subject to the laws of quantum mechanics, and you are trying to understand how it travels through the machine. The goal is to understand how quantum information travels through spacetime. In fact, we think that the geometry of spacetime itself is reflecting properties of this quantum information.
Ultimately, we want to understand a black hole as a system that obeys the rules of quantum mechanics, and how those rules are consistent with the rules of gravity. They seem to be very different, and there are some paradoxes that haven't been resolved yet. We are trying to understand how the view of black holes as a quantum computer is consistent and compatible with the view of black holes that comes from Einstein's theory of general relativity. ––Kelly Devine Thomas, Editorial Director