Black Holes and the Butterfly Effect
One of the surprising things about chaos is that it took so long for physicists to appreciate how common it is. This is despite the fact that people seem to come naturally programmed with intuition for the basic phenomenon: that small changes to the state of a complicated system can lead to dramatic changes a short while later. This idea is often referred to as the butterfly effect, and it was on display in creative works like the movie It’s a Wonderful Life (1946) and the science fiction short story “A Sound of Thunder” (1952) even before it became widely appreciated in physics.
Part of the reason for this historical blind spot is that chaotic systems tend to be difficult to analyze. So, even though non-chaotic systems (where small changes don’t lead to large effects) are rare, there is a strong selection effect in favor of studying them. This changed in a fundamental way in the 1960s, with the help of computers. Computers are great at solving the equations of classical physics, and numerical study of many different systems has led to a beautiful and rich phenomenology of classical chaos.
Unfortunately, computers do not have the same power at simulating quantum systems, particularly quantum field theories (theories of interacting quantum particles). This is because the memory and central processing unit requirements of simulating a quantum system increase exponentially with the number of particles involved. To a large extent, our understanding of these systems is therefore limited to problems that can be solved by hand. And, just as in classical physics, these normally do not include systems complicated enough to exhibit much chaos. So we are more or less still in the dark when it comes to quantum chaos.
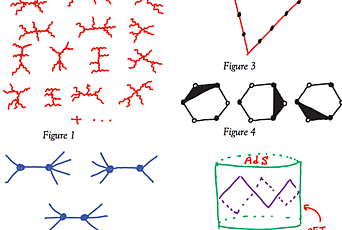
A small region of insight is provided by the AdS/CFT (anti-de Sitter/conformal field theory) correspondence, proposed by IAS Professor Juan Maldacena almost twenty years ago. A special case of this correspondence is an exact equivalence between a nicely chaotic quantum field theory (the strongly coupled large N super Yang-Mills theory at finite temperature) and one of the simplest objects in general relativity: a black hole. This means that for this example, it is possible to analyze chaotic dynamics in a quantum field theory (hard) using black hole dynamics (easy-ish).
Before we get any further, it is helpful to have in mind a thought experiment that tests for the butterfly effect. We can illustrate this by thinking about an unusual state for a familiar chaotic system: a bath of water. Imagine that we have a full tub in a very special configuration where, if we leave it alone, a little whirlpool will spontaneously form somewhere on the surface a few minutes from now. Instead of leaving it alone, we could add an extra water molecule somewhere else in the tub and then wait and check for the whirlpool. Such a very tiny change to the overall state of the system would get amplified over time, and at the expected moment a few minutes from now, the whirlpool would fail to appear. This is a sharp diagnostic of chaos.
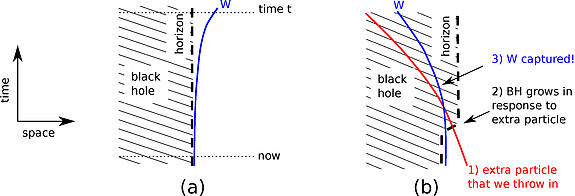
Now let’s run the same experiment, replacing the bath of water with a black hole. First, one needs an analogue of the state where a whirlpool will form in a few minutes. The simplest thing is to consider a state where the black hole will emit an extra photon at some time t a few minutes in the future. Let’s call the extra photon W for “whirlpool.” Then, before it emerges, W will be very close to the horizon (the point of no return for the black hole), traveling on a trajectory where it will just barely manage to escape. If t is far in the future, trajectories of this type hug the horizon very closely for a while, before finally pulling away and emerging to safety at time t. This is illustrated in part (a) of the drawing.
For the second step of the thought experiment, we are supposed to add a small perturbation to the system. Here, the simplest thing is to imagine that we just throw an extra particle into the black hole. This would have the effect of making it a tiny bit bigger. In particular, the extra particle would move the horizon out by a small amount. Now, the key point is the following: if the time t is sufficiently far in the future, then at time zero W would be so close to the horizon that even this small increase in mass would be enough for the black hole to capture W. The whirlpool will not form! This is illustrated in part (b) of the same drawing.
One can analyze this in more detail, and find that the strength of the effect of the perturbation on the “whirlpool” W grows exponentially with the time difference t, as eλt with λ given by 2π times the temperature. In work with Maldacena and with Steve Shenker from Stanford University, we showed that this rate of exponential growth is the fastest possible in quantum mechanics. So, although it sounded like a very simple effect, this is actually a manifestation of the strongest chaos allowed by the laws of nature. (This is part of a pattern of hypercompetitive behavior that has been observed in black holes before: it seems that they have to be the best at everything they do.)
It seems that black holes have to be the best at everything they do.
In a surprising twist, Alexei Kitaev from Caltech found a quantum system where it is possible to analyze this type of thought experiment by direct calculation, without appealing to the AdS/CFT correspondence and black holes. And Kitaev found that his system has the same rate of growth that we described above: 2π times the temperature. This suggests the interesting possibility that the Kitaev model might be a black hole in disguise.
For me, this is tremendously exciting, because having a solvable description of a black hole might help shed light on some of the deep mysteries about quantum gravity. Normally, (as in the discussion above) one uses the AdS/CFT correspondence to learn about quantum field theories using gravity and black holes. But this solvable system might make it possible to turn the arrows around and learn about gravity using Kitaev’s model. I should mention that there has been another twist, which is that closer inspection has revealed that the dual description is a black hole in a rather unfamiliar theory of quantum gravity. But many of us remain hopeful that it will be possible to learn some lessons from the model.
The lesson one would most like to learn is how to describe the region behind the horizon of the black hole using the dual quantum system. In the analogy to the bath of water, this might be a bit like asking for a mathematical theory of whirlpools that never quite form. It is a problem so stubborn that it has led some researchers to believe that the region doesn’t exist at all! But the concentration of interest in this problem at the IAS makes me optimistic that we will soon know the answer. Perhaps we should take a lesson from the past and look for hints in the science fiction literature.