From the Motion of Planets to Quantum Field Theory

What do the motion of the planets in our solar system, the energy levels of the hydrogen atom, and the interactions between subatomic particles have in common? Surprisingly, they are all governed by the same hidden symmetry principles. This is what Simon Caron-Huot (now Assistant Professor at the Niels-Bohr Institute, Copenhagen) and I found in recent work done as Members at the Institute.

Symmetry is a very important notion in physics, for mainly two reasons. On the one hand, systems with a lot of symmetry are usually easier to solve and study, so that key properties can be understood analytically. On the other hand, and more fundamentally, in the development of physics, symmetry principles have often been a successful guiding principle toward theories relevant for describing nature. An example is Einstein’s equivalence principle that led to the development of general relativity.

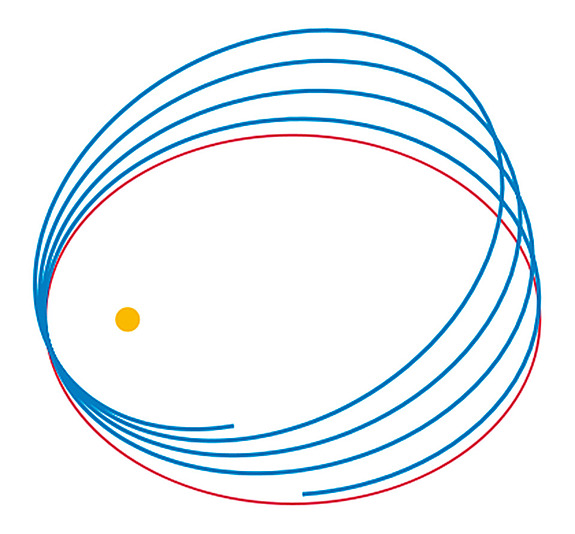
What is the hidden symmetry underlying the motion of the planets, such as the Sun and the Earth? The answer to this question is important for the Kepler problem, i.e., the question of how to predict the position and velocity of two bodies, given some initial conditions. (It should be noted that physicists often use the word “problem” not in the standard meaning, which has a negative connotation; rather, it should be thought of in a positive sense, as an interesting challenge.) The motion is governed by Newton’s laws, which tell us, in particular, that the gravitational force between two objects depends only on their relative distance. From this, it follows that the orbits lie in a plane. However, observing the trajectories more closely, one sees that they form ellipses that do not precess with time. In other words, the orientation of the ellipses does not change, and hence the orbits are closed. This regularity is a hint for a hidden symmetry, which in turn implies a constant of motion. Indeed, a certain vector, named after Laplace-Runge-Lenz (LRL), does not change with time (see figure).¹ It points toward the perihelion of the ellipse, i.e., the point of the orbit where the Earth comes closest to the Sun, and its conservation explains the regularity of the orbits that we observe.

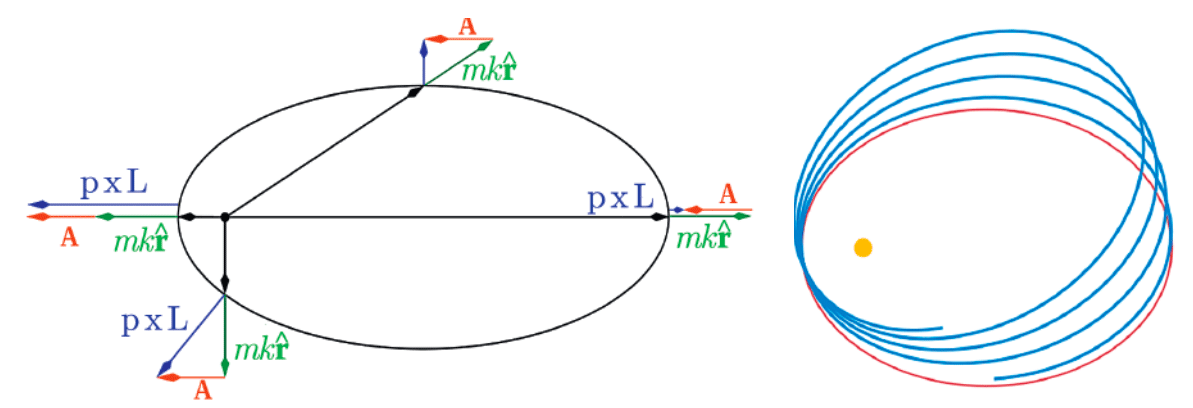
This is an example where the laws of nature have an exact symmetry. This often allows one to understand the properties of a theory better, or to perform exact calculations. Sometimes symmetries are only approximate, but can still be very useful. In the present example, the symmetry is broken by other effects, such as gravitational interactions with other planets or corrections coming from general relativity. Whenever the latter can be treated as a perturbation, the exact solution based on the symmetry is a good starting point for the description of the full system.

At atomic scales (when describing molecules, for example), classical mechanics needs to be replaced by quantum dynamics, which was developed in the first part of the twentieth century. The hydrogen atom, consisting of a positively charged proton and a negatively charged electron, can be thought of as the quantum mechanical version of the Kepler problem. In quantum mechanics, positions and momenta are replaced by operators (or matrices) that in general do not commute––this is related to Heisenberg’s uncertainty principle, which says that the position and the velocity of a particle cannot be known at the same time. A quantum dynamical system is described by a so-called Hamiltonian, whose eigenvalues are the allowed energy levels. It turns out that a suitable quantum version of the LRL vector commutes with the Hamiltonian, meaning it is a conserved quantity in quantum mechanics. This fact was famously used in the early days of quantum mechanics by Wolfgang Pauli to compute the spectrum of the hydrogen atom,² in agreement with earlier experiments. The fact that this calculation could be done even before quantum mechanics was fully developed, meaning before the discovery of the Schrödinger equation, further emphasizes the usefulness of the symmetry.

Going to subatomic scales, quantum mechanics, which describes a system with a fixed number of states, is no longer adequate. This can be understood intuitively by Einstein’s famous equation stating the equivalence of energy and matter. At high enough energies, particles can be produced and annihilated. Quantum field theory (QFT), developed in the second part of the twentieth century, is appropriate to describe such systems. Its Feynman diagrams can be used to visualize how particles interact with each other.

The so-called Standard Model of elementary particles is based on a specific QFT called quantum chromodynamics (QCD). It is used to successfully describe properties and interactions of elementary particles such as electrons, photons, quarks, and gluons. The discovery of the Higgs boson at the Large Hadron Collider (LHC) at CERN was made possible, on the theoretical side, by predictions of this theory.

Quantum field theory, and in particular QCD, is very complicated, and only in very special cases can exact solutions be obtained. One might ask whether there is an idealized version of QCD that is the analogue to the hydrogen atom in quantum mechanics, in the sense that it can be exactly solved. When looking for such a special quantum field theory, a natural question is whether the LRL symmetry can be transferred to quantum field theory.

First hints can be gleaned from a model for electron-proton boundstates analyzed by Richard Cutkosky and Gian Carlo Wick (Member 1953) in the 1950s.³ Their model, based on a certain approximation that keeps only subsets of Feynman diagrams, indeed has an extra symmetry that can be traced back to the LRL vector. However, the approximation they used is an ad hoc one and neglects important multi-particle effects, for example. This leads to the question of whether this model could be embedded in a fully consistent quantum field theory.

The answer to this question arose while studying a supersymmetric version of QCD called N=4 Super Yang-Mills. This theory was previously found to have an unexpected hidden symmetry, dubbed dual conformal symmetry, in the so-called planar limit, where only planar Feynman diagrams are kept. This can be done in a consistent way. Simon and I considered hydrogen-like bound states of two massive particles within this theory, similar to the ones considered by Cutkosky and Wick, but including multi-particle interactions. We showed that the dual conformal symmetry is directly related to the classical LRL symmetry.⁴

Just like in the Kepler and hydrogen examples, the symmetry helps simplify calculations dramatically. We were able to use the latter to map the calculation of the bound-state energy levels to a much simpler situation. This makes the problem amenable to powerful integrability techniques that were recently developed and that are applicable even in the strongly coupled regime. This constitutes an important step toward the first analytic solution of a bound-state problem in a four-dimensional Yang-Mills theory.

This research also suggests a number of interesting questions:

• Is N=4 Super Yang-Mills the unique quantum field theory having an LRL symmetry?
• Is there a generalization of this symmetry to non-planar corrections?
• In quantum mechanics, with hindsight, it is possible to choose variables that make the LRL symmetry obvious by rewriting the Kepler problem as a four-dimensional harmonic oscillator. Is there a reformulation of quantum field theory that makes the hidden symmetry manifest?

In a broader context, N=4 Super Yang-Mills can be thought of as a toy model of QCD. It is a toy model not in the sense of particle phenomenology but for the complicated calculations necessary to make predictions from quantum field theory. For example, theoretically describing collider experiments, such as the ones being conducted at the LHC, requires scattering amplitudes that can be computed from QFT. Studying the supersymmetric model already has led to numerous important insights and new techniques. This line of research continues to be a very rich enterprise, constantly unveiling new surprises about quantum field theory and new tools for performing QCD calculations that are relevant for LHC physics.

A concrete recent example of this has to do with the notoriously difficult Feynman integrals appearing in perturbative QFT. A key idea, developed by IAS Professor Nima Arkani-Hamed and his collaborators, is that the singularity structure of the Feynman integrand can be used to predict properties of the integrated answer.⁵ Through discussions with Nima, and playing with examples, I realized that many of the concepts could be applied beyond N=4 Super Yang-Mills. This led me to propose a new method for computing Feynman integrals that is by now widely used.⁶

The IAS is one of the few places in the world where postdoctoral researchers find an ideal environment for research without teaching obligations, deadlines, and so on. Indeed, not being constrained to follow a specific, predetermined research program is crucial for making new, unexpected discoveries. Perhaps the IAS could be compared to a parallel universe, or a protective bubble, where speculative new ideas can be developed and strengthened to the point where they can survive the harsh real world outside. This was certainly the case for the new techniques I just mentioned.

I greatly enjoyed the many opportunities to discuss my research with other IAS Members and Faculty at lunch, in the wonderful discussion areas in Bloomberg Hall, at tea, and elsewhere on the IAS campus. With so many possibilities for discussions, it is hard to remember how exactly Simon and I began working together, but it would not surprise me if our project started somewhere between tea time or a game of tennis at the IAS courts.