Using Computation to Understand Why Black Holes Shine

The following article is based on a virtual talk given to the Trustees and friends of the Institute.

Let me begin at the beginning with the basic question of: what is a black hole? In perhaps the simplest terms, a black hole is a collapsed object in which matter is so dense that not even light can escape from its surface. The term black hole was actually coined by John Wheeler, who at the time was a professor in the physics department here at Princeton University, and it’s really a very appropriate term.

Remarkably, black holes were once thought to be only a theoretical construct of general relativity. The solutions to Einstein’s equations that predict black holes were quite surprising at first, and were thought to be a quirk of the mathematics of general relativity. What’s even more amazing is that today we know for certain that black holes actually exist in nature, in fact this year’s Nobel Prize was awarded for the certain proof that there is a black hole at the center of our own Milky Way galaxy (as I’ll describe in a minute). In 2017, the Nobel Prize was awarded for the discovery of gravitational waves produced by merging black holes. So they are no longer just a mathematical quirk in general relativity.

How do we know there is a black hole at the center of the Milky Way? Just as we can use Kepler’s laws of motion to measure the mass of the sun by the orbits of its planets, we can measure the mass of a black hole by the orbits of the stars going around it. Recording the positions of stars at the center of the Galaxy over the last couple of decades (below) has shown that they are zipping around some unseen point mass that contains 4.1-million-solar masses of matter, but is smaller than the Earth’s orbit around the Sun. We know of no object other than a black hole that could be so small with that much mass. Most astronomers consider this pretty direct evidence of a black hole at the senter of the Milky Way.

Orbits of stars surrounding our galaxy’s black hole.

Are there black holes at the center of other galaxies? If you look closely at an optical image of the M87 galaxy (see top of page), you can see this kind of smudge of blue light coming out of the center. Back when the first high-quality photographic images of this galaxy were made in 1919, it was noted that this “curious straight ray” was coming from the center of this galaxy, M87. Nowadays, using radio telescopes, we’ve discovered that this straight ray of light is actually a narrow jet of matter flowing out of the center of M87 at very close to the speed of light. We think the only kind of object that can create such powerful relativistic jets are black holes. So that’s indirect evidence of a black hole at the center of M87.

Event Horizon Telescope Collaboration

The first image of a black hole from Event Horizon Telescope observations of the center of the galaxy M87

But of course, direct proof of the black hole at the center of M87 has recently come from the Event Horizon Telescope (EHT). It is a collection of radio telescopes that work together to make an image with the same resolution as a single telescope the size of the entire Earth. And with such high resolution, we’ve actually resolved that shadow of the event horizon of the black hole in M87 (see above). One of the members in the Astrophysics group at the IAS, Lia Medeiros, has been very involved in the work of the EHT and the production of this image.

The black hole in the M87 galaxy is not dark in the EHT image, because what we’re observing is not the black hole per se, but hot plasma that’s falling into the black hole (see below). When accreting plasma—a gas of charged particles, electrons, and protons—falls into the black hole and gets compressed, it heats up, just like how when you pump up a bicycle tire it gets warm from adiabatic compression. In addition, as the plasma falls in it releases gravitational energy, and this energy gets turned into heat. As the electrons in the plasma get hot, they start to emit photons (light), which is what we see in the EHT image.

Event Horizon Telescope/Hotaka Shiokawa

Computational model of plasma accreting into a black hole

Where does computation come into this story? Computational methods are absolutely crucial for this work in two ways. The first is for reducing the actual data itself. As you can imagine, the EHT is a complicated instrument which generates terabytes of data. Reducing this data and producing the image that you see is a challenging computational problem in data science. Secondly, in order to produce and interpret the image and to measure things like the mass and spin of the black hole, models of the plasma flowing into the black hole are needed. Generating those models requires very sophisticated computational methods.

Methods for computing theoretical models of the plasma flow into black holes is in fact one of my main areas of research. How are such computations performed? The mathematical equations that describe the time evolution of basic properties of the plasma like density, momentum, and energy are a well-known set of differential equations. If you have some regions of space in which you want to model the plasma dynamics, you break that space up into discrete cells. You might have millions or billions of these cells in a single calculation. In each cell, you store the mass, energy, momentum, all of the conserved quantities. Then you update these quantities according to an approximation to the underlying differential equations that you can solve on a computer. This approximation tells you how to update the mass, momentum, and energy in every cell, which gives you the time evolution of the plasma.

And this is where algorithms come into play. The accuracy of the numerical methods used to find approximate solutions to the underlying differential equations is measured by something called the rate of convergence. This rate measures how quickly the error in the solution decreases as you add more cells. If the error drops by a factor of two when you double the number of cells, the method is called first-order. If it drops by four when you double the number, the method is called second-order, and so on. So higher methods are more accurate. For some problems you would need a resolution that is one hundred times higher per dimension to get the same accuracy with a second-order algorithm as you would need for a fourth-order algorithm. And because of the way the cost of the calculations increases with resolution, one hundred times more cells per dimension is a hundred million times more expensive. But higher-order methods are also more complicated, and harder to program on a computer, which is why they have only recently begun to become popular.

In fact, the increase in computer power over the last few decades is not enough to beat the increase in accuracy you get from using better, that is to say higher-order, algorithms. So that’s why algorithms always win. They always lead to a much bigger increase in accuracy than just making the computer faster. Smart algorithms allow calculations that could have never been done even on the world’s fastest computer today. And that’s why developing new algorithms is so important for so many problems in science in general, not just astrophysics.

____________

Let’s return to talking about making images of black holes from the plasma that they are accreting. In the case of our own black hole at the center of the Milky Way, the first question you might ask is, where does all this plasma come from? We know for the case of the black hole in our own galaxy, it comes from the stars near the galactic center. Some of the stars that orbit very close to the galactic center have very powerful outflows, winds just like the sun has a wind. But these stars have much more powerful winds than the sun. The outflows from all of these different stars collide with each other, and when they collide that produces shock waves that fill the region around the black hole with shocked gas from the stellar winds. You can actually see this material in X-ray images of the galactic center as a bright bubble of hot plasma formed by winds from all these stars. The black hole at the center of the galaxy is accreting this X-ray–emitting plasma formed by these stellar winds.

Using the same numerical methods we use to model the accretion of plasma into the black hole itself, we can actually model the dynamics of the winds emanating from these stars directly, and follow the shocks formed as the winds collide with each other. That allows us to understand how the stars feed plasma into the black hole at the center.

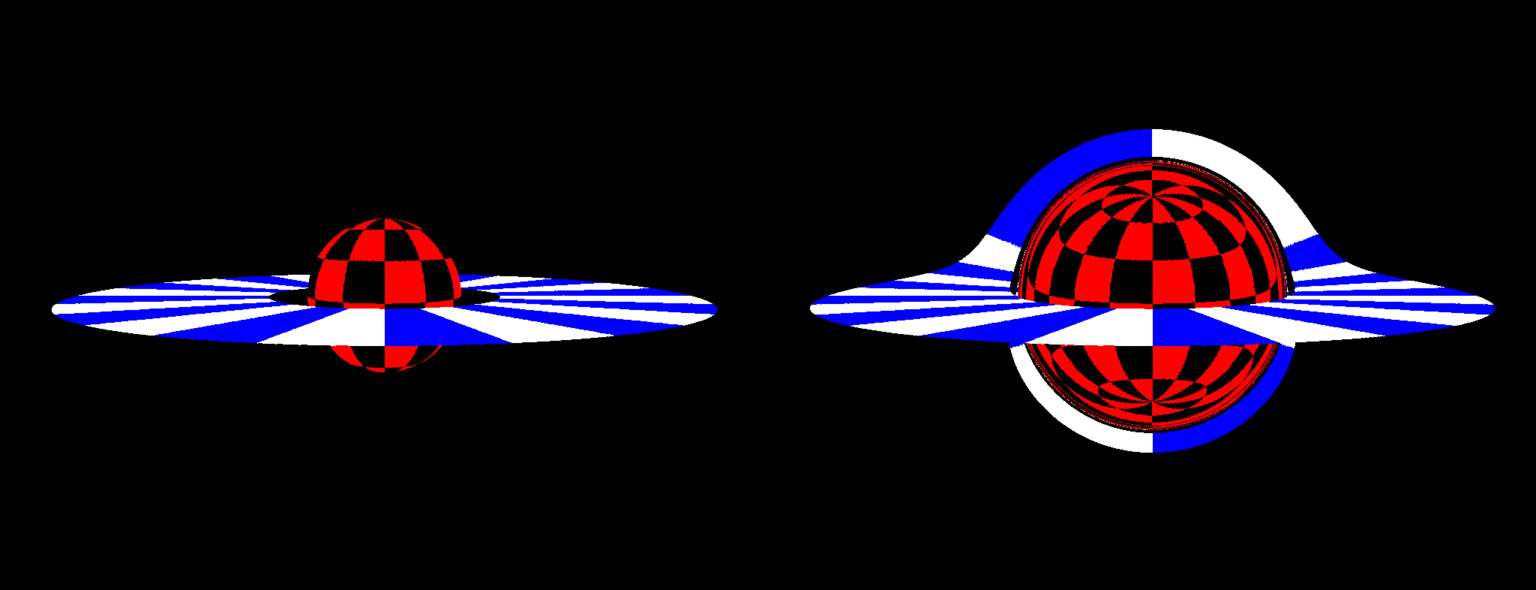
Finally, there’s one more interesting ingredient that has to be included in modeling the EHT image, which is how light emitted by plasma is affected by the gravitational field of the black hole. Near a black hole, light no longer travels on straight lines, but light rays are bent by the curvature of spacetime. To make this more concrete, if you imagine a thin disc of plasma orbiting around a point mass in non-relativistic Newtonian gravity, you would see the familiar image on the left (see below). It looks a lot like how Saturn’s rings look to an observer from Earth. In relativity, however, this thin disc looks like the right image. Near the black hole space-time is curved, so that photons travel on curved paths on their way to you. Photons emitted from the back of the disk are bent over the top of the black hole, and then focused towards the direction we are viewing from. This means the back side of the disk appears to be located just above the top of the black hole. Incorporating these relativistic effects is incredibly important because it makes the image of a disk around a black hole look completely different compared to a disk around a normal star.

Riccardo Antonelli

Appearance of a thin disc around a point mass in Newtonian gravity (left) and in general relativity (right). The latter demonstrates how light rays are bent in GR.

Going forward, we’re going to learn a lot of plasma physics from the current and future observations. EHT is a wonderful experiment to understand general relativity and black holes, but I think it’s also a much more interesting experiment to understand plasma astrophysics in the relativistic regime, because the plasma is what we actually see. There are many more physical effects to be included in future models. For example, the temperature of the ions and electrons in the plasma are probably different, and that changes the image. The radiation produced by the plasma also affects its dynamics, and therefore that can change the image compared to a model that does not include radiation. All of these things need to be incorporated in future models. We know the equations to solve, we just need to write the software and do the modeling properly. It’s going to keep us busy for many years in the future. Ultimately, we hope to learn a lot more about black holes, and how they affect their environment, from both future observations and future numerical models.