The Universe Speaks in Numbers
"Multi-faceted gems, each with crystalline symmetry that gives them an unexpected mathematical beauty”—that is how the physicist Lance Dixon describes the mathematical objects used to predict what happens when nature’s fundamental particles scatter off each other. These particles—including the subnuclear quarks and gluons—have no shape or size, so such scatterings might be regarded as one step up from nothingness.
Interest in scattering amplitudes among physicists has increased rapidly in recent decades. Theoreticians need a clear understanding of these amplitudes to interpret data from the ultra-high-energy collisions between protons at CERN’s Large Hadron Collider—in essence, these collisions involve scatterings of the quarks and gluons inside the protons. The improved understanding of these collisions helped to enable the experimenters’ great discovery of the Higgs particle in 2012.
One of the biggest leaps forward in our understanding of these amplitudes took place at the Institute for Advanced Study in the fall of 2003, when Edward Witten discovered a new approach to the subject, based on Roger Penrose’s twistors. Penrose still believed that these mathematical objects, which he had discovered in the 1960s, offer the best hope of supplying the basis of a fundamental theory of nature. But they had yet to become part of mainstream physics, and most theorists regarded them as merely a mathematical curiosity. Witten’s work propelled them into the mainstream of theoretical physics, generated new lines of research, and opened up new ways of thinking about scattering in the subnuclear domain.
Using Penrose’s twistors, Witten set up a new type of string theory. Each twistor describes the history of a massless particle as it moves through spacetime—a challenging concept that Witten had been struggling with for several years and occasionally used in his papers. Witten had now used twistors to come up with a new string theory that did not apply in higher dimensions but was framed in terms of ordinary, four-dimensional spacetime.
By mid-December 2003, when many people in the West were following the capture of Saddam Hussein, many theoreticians were—for the first time—fixated on twistors. Although Penrose didn’t “completely buy” the new theory, he was delighted to see twistors propelled into the mainstream of science. Among the readers who wolfed down Witten’s paper was the Harvard-based theorist Nima Arkani-Hamed. “The twistor-strings paper was wilder and more transgressive than most ‘Edward-style’ presentations we’re used to, where everything is laid out logically and understood perfectly.” It was as if, out of the blue, Bach had written a piece of bebop.
One of the first physicists to appreciate the power of this method was Freddy Cachazo, an impressively talented young Venezuelan field theorist who had an office on the same corridor of the Institute as Witten. “We all knew Edward was on to something,” Cachazo recalls. “He was working alone, crazy hours, late into the night, at weekends, but none of us knew what he was doing.” Cachazo found out after Witten walked into his office one afternoon and asked him whether he “would give him a hand with a few calculations that required the use of the Mathematica software program.” Within a week, Cachazo’s number crunching was producing a stream of dazzling results.
For a few months, twistor string theory was a red-hot topic—after decades in the dark wings of theoretical physics, Witten had thrust it into the limelight. Among the converts to the twistor approach at the Institute were Ruth Britto and Bo Feng, two young researchers who had known Cachazo since their student days. Building on Witten’s edifice, the three theorists quickly developed a new set of mathematical relationships between the scattering amplitudes in the theory.
Sensing that there was more to learn from this approach, Witten joined the trio of young theorists. Within a few weeks, they had a resounding success: they discovered a surprisingly neat way to calculate complicated scattering amplitudes by “building” them up from much simpler ones, using a set of straightforward rules, with twistors apparently less central to the formalism than most physicists had first believed. Central to the method was a clever application of a classic theorem of complex functions first proved almost two centuries earlier, by the French mathematician Augustin-Louis Cauchy. Witten and his colleagues used a famous theorem discovered by Cauchy to develop a set of elegant formulae that applied not only to quarks and gluons but, surprisingly, to all the other subatomic particles in the Standard Model, and even described their motion in higher spacetime dimensions. Experts in scattering amplitudes regarded the formulae as a sensation, a genuine breakthrough. In a lively seminar given by Cachazo at Harvard, he caught the attention of Arkani-Hamed, who later said, “I was blown away. I had no idea that scattering amplitudes were teaching us so much about field theory.” Within a few days, he had decided “to become a graduate student all over again” and learn the subject from Cachazo. Within a few months, they had begun a collaboration that eventually led not only to new insights into collisions between subatomic particles but also, unexpectedly, to some of the frontiers of mathematics that had previously been of little or no interest to physicists.
In early 2008, when Nima Arkani-Hamed joined the Faculty at the Institute for Advanced Study in Princeton, he and Cachazo were deep into their collaboration. By the end of the year, a few weeks after Barack Obama’s election to the U.S. presidency, they were exploring a new approach to scattering theory suggested by Oxford theoretician Andrew Hodges.
He was best known for his classic biography of the computer science pioneer Alan Turing, a book that later inspired the Oscar-winning script for The Imitation Game. Hodges had begun to write the book in 1977, two years after he had completed his Ph.D., advised by Penrose, on twistor diagrams. These diagrams were, roughly speaking, the analogue in twistor theory of Feynman diagrams in conventional field theory and were another of Penrose’s innovations. No particle physicist took much notice of Hodges’s diagrams, partly because they were bedeviled by mathematical difficulties. Almost two decades later, Hodges claimed that twistor diagrams supplied by far the easiest way of understanding the relationships between scattering amplitudes written down by Witten and his three young collaborators. Hardly anyone took Hodges seriously—for almost two years, his paper lay unread on the desk of Arkani-Hamed, who could not make up his mind whether it “was the work of a crank or a genius.”
But only a few months after Arkani-Hamed began working in earnest on scattering amplitudes, he was clear that Hodges was anything but a crank. “By bending our way of thinking to fit his,” Arkani-Hamed later said, “Freddy and I found ourselves making pretty good progress understanding how twistors can help understand scattering amplitudes.”
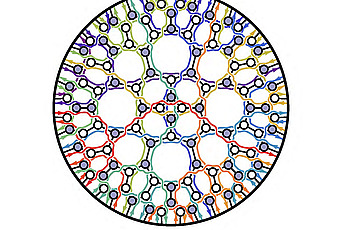
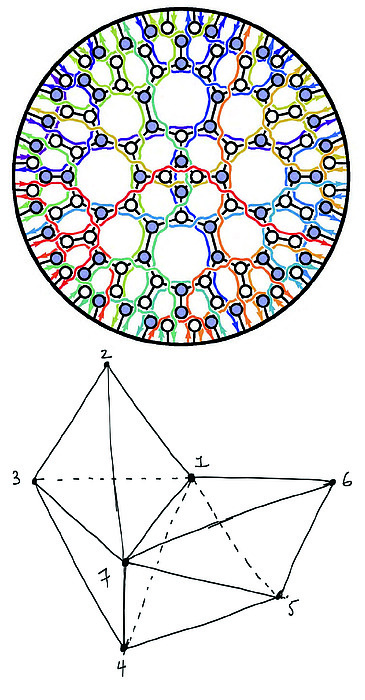
On the morning of April 30, 2009, Arkani-Hamed received what he later described as “a bolt from the blue.” It was an email from David Skinner informing him of several breakthroughs by him and his colleagues, notably one by Hodges, who had proposed a new way of calculating scattering amplitudes for gluons. Instead of adding together a series of contributions, each generated by a Feynman diagram, Hodges suggested that in some cases the amplitude might be interpreted as the volume of a type of abstract object. This object is known as a polytope, an assembly of abstract “triangles” that fit together to form a volume in higher-dimensional space. In ordinary three-dimensional space, these objects are analogous to popular Christmas decorations shaped like a multipointed star.
Arkani-Hamed and Cachazo had a hunch that they needed some new mathematical perspective to make progress. In late spring of 2009, they consulted a few books that they guessed might be relevant, including The Principles of Algebraic Geometry, a tome written thirty years before by the mathematicians Phillip Griffiths and Joe Harris. On the morning of June 10, Cachazo made a breakthrough. While reading the first chapter of Griffiths and Harris’s book—one of only two mathematics books he owned—he saw a simple matrix—an array of mathematical variables—that looked exactly like the one he and Arkani-Hamed were working on. This object, Cachazo read, is an expression of what mathematicians describe as the Grassmannian, familiar to few theoretical physicists but well known among pure mathematicians. This mathematical construction was first written down in 1844 by the school teacher and ordained minister Hermann Grassmann in his book Ausdehnungslehre, largely ignored at the time, though subsequent generations of mathematicians regarded it as a visionary masterwork.
“I was so excited that I wanted to tell everyone,” Cachazo later recalled. But he kept his excitement to himself for a few hours, studied the pages of Griffiths and Harris’s book, and convinced himself that this was just the mathematics he and Arkani-Hamed needed. “I wanted Nima to feel the same thrill as I had, so I decided to send him a cryptic email” that afternoon, he remembered: “Look at page 193 of Griffiths and Harris!” Three hours later, Arkani-Hamed emailed his reply: “Well now!! This is amazing. . . .” The Grassmannian appeared to be perfectly suited to describing what happens when gluons scatter off each other. In the case of two gluons producing five gluons, the motion of all the particles can be described using an array of numbers—a matrix—with seven rows (one for each gluon) and four columns (one for each dimension of spacetime). Grassmann’s mathematics enables physicists to handle all the quantities in the matrix with ease. Even better, the method was completely general: it didn’t apply to a particular number of gluons but to any number of them. As Arkani-Hamed says, “This 160-year-old mathematics was sitting there on the shelf, as if Grassmann had wanted to help us describe gluonic scattering in the most general possible way, about 125 years before anyone had even conceived of gluons.”
Arkani-Hamed, Cachazo, and their colleagues were elated. Within a few days, the Grassmannian had enabled them to generate mathematically every one of the main contributions to the scattering amplitude that describes gluonic scattering. In one fell swoop, this mathematical framework enabled a unified method of describing gluonic scattering—including twistor string theory, Hodges’s recent discoveries, and even the formula discovered by Witten and his three young collaborators.
Soon thereafter, Arkani-Hamed, Cachazo, and their collaborators posted online a paper that demonstrated how Grassmannian mathematics supplied a unifying understanding of all of Hodges’s twistor diagrams. Arkani-Hamed knew he and his colleagues had only scratched the surface of the subject. One serious problem with the Grassmannian method was that it yielded too much information: it contained all the mathematical contributions needed to describe the gluonic scattering amplitudes, but no rule for how to combine them into the separate amplitudes. It was as if physicists had all the pieces they needed to solve a jigsaw puzzle without knowing the puzzle’s shape.
Lost again, Arkani-Hamed and his colleagues changed tack. They decided to try to understand the behavior of the gluons via the simplest viable description, using what is sometimes known as the Superglue Model. This mathematical construction did not attempt to describe gluons in the real world to high accuracy but gave a means of studying the most important aspects of their behavior using mathematics with an exceptionally high degree of symmetry, which made calculations relatively easy. This model’s predictions for scattering at ultra-high energies are identical to those of the experimentally well-established gauge theory of strong interactions, thus providing a secure link with the real world.
By applying Grassmannian mathematics to the Superglue Model, Arkani-Hamed and his collaborators hoped to be rewarded by a revelation. But they got nowhere and decided that it was time they sought help to come to grips with the mathematics, which looked forbiddingly complicated. In a series of meetings, Arkani-Hamed and his colleagues discussed their mathematical challenges with some of the Institute’s mathematicians—including Pierre Deligne and Bob MacPherson—and Sasha Goncharov, a Yale expert in algebraic geometry. To help get the conversation moving, Witten attended the first meeting, partly to help translate between the languages of scattering amplitude physics and the mathematical concepts that might be relevant. Afterwards, the mathematicians and theoreticians met regularly, with Deligne regularly placing a wodge of clarifying mathematical notes in Arkani-Hamed’s mailbox—“They were solid gold for us,” Arkani-Hamed later said.
In the early summer of 2011, the penny finally dropped. To understand what happens when gluons scatter off each other, the theorists did not need to use the entire Grassmannian object but only a part of it, the so-called positive Grassmannian. For months, Arkani-Hamed and his collaborators tried to incorporate Hodges’s idea that scattering amplitudes could be calculated as “volumes” into the positive-Grassmannian framework. They struggled to make headway. One of Arkani-Hamed’s students, Jacob Bourjaily, remembers that the group’s working practices were as exhilarating as they were exhausting: “Nima likes to pull quite a lot of ‘all-nighters,’ fueled by espressos, Diet Cokes, and nachos. . . . The sessions often ended at dawn when we fetched up in a local diner for a communal breakfast, though we were still talking physics, non-stop.”
Convinced that they still needed a better understanding of the underlying mathematics, in the autumn of 2011, Arkani-Hamed, Bourjaily, and their colleagues secured a meeting with Alexander Postnikov, the blue-chip Grassmannian expert at the Massachusetts Institute of Technology. The encounter turned out to be a revelation. During the intense discussions in Postnikov’s shambolic office, and later over lunch in the nearby canteen, it gradually emerged that they were working on the same thing. At one point, Postnikov pulled out some diagrams of a type that he had not previously mentioned, only for Arkani-Hamed and his colleagues to see—to their astonishment—that they were identical to ones that they had been using for months.
In a rally of instant messages on a summer Saturday afternoon in 2013, Arkani-Hamed and his graduate student Jaroslav Trnka decided on a name for the new object: the amplituhedron, which they used in December 2013 as the title of the paper in which the object first appeared. The “amplituhedron picture” of predicting what happens when two gluons collide is potentially revolutionary. In Feynman’s method, the interactions between gluons take place only at points in spacetime (so-called locality), and it is assumed at the beginning that the total probability of all outcomes of a collision between two gluons must be precisely one (unitarity). But, in Arkani-Hamed and Trnka’s amplituhedron method, the scattering is described in a completely different way: the locality and unitarity emerge from the mathematical formulae in the final stage of the calculation. Arkani-Hamed and Trnka had discovered the first example of a structure in which “space and time” and quantum mechanics are not fundamental. Arkani-Hamed later told me, “This is a concrete example of a way in which the physics we normally associate with spacetime and quantum mechanics arises from -something more basic.”
The amplituhedron—sometimes referred to as a quantum jewel—caused quite a stir among theoretical physicists. Some critics, however, cautioned that the amplituhedron might just be an artefact of the Superglue Model, an approximation to reality, and may have nothing to do with the scattering of real particles. Time will tell. Arkani-Hamed later told me that he is increasingly confident that the significance of the amplituhedron has yet to be fully understood. One sign of this is that, since the object’s discovery in scattering-amplitudes theory, it has also cropped up in three other parts of physics: cosmology, quantum theories of gravity, and very general classes of field theory. No one understands why, Arkani-Hamed says, though he is confident that the reason for this will eventually become clear. He is convinced that the mathematics that he and his colleagues are using—much of it rarely (if ever) before used in fundamental physics—will be of fundamental importance to describing nature. “This is not the mathematics of smooth surfaces that works so well in string theory, for example,” he says. “It’s mathematics much more closely linked to whole numbers.”
The amplituhedron was a gift for mathematicians. One of the reasons it was so fascinating to them was that they could have discovered it long before, by building logically on Grassmann’s idea and with no reference to the real world. But it fell to physicists to unearth the object, steered by a wish to understand gluonic scattering and using the twin constraints of quantum mechanics and the special theory of relativity. These theories have been the sturdy guiderails of theoretical physics for almost a century and have generated a wealth of new physical ideas, together with fascinating connections with advanced mathematics. The field of scattering amplitudes exemplifies the symbiosis between physics and mathematics at the frontiers they share.