Singular Adventures of Baron Bourgain in the Labyrinth of the Continuum

There are two labyrinths of the human mind: one concerns the composition of the continuum, and the other the nature of freedom, and both spring from the same source—the infinite. —Baron von Leibniz
"During World War II, when von Neumann was working on the design of nuclear weapons, he came to the conclusion that analytical methods were inadequate to the task, and that the only way to deal with equations of continuum mechanics is to discretize them. ... It is to this task that von Neumann devoted his energies after the war." —Peter Lax
Overture
Baron Bourgain, the IBM von Neumann Professor in the School of Mathematics at the Institute for Advanced Study (IAS), is one of the most original, penetrating, and versatile analytical minds of our troubled times, justly celebrated and revered without reservations.
While he rejected outright the suggestion of a sixtieth birthday conference, a proposal to have a gathering occasioned by the publication of his 500th paper was not immediately dismissed —the conference “Analysis and Beyond: Celebrating Jean Bourgain’s Work and its Impact” took place at the IAS in Princeton on May 21–24, 2016. The conference talks (all of which were videotaped) are a tribute to the depth and breadth of Bourgain’s work and its singular and transcendent impact on the whole of our discipline. The beauty and power of the first result highlighted by Jean’s hand on the conference poster is apparent from reading the splendid paper by Andrea Nahmod in the Bulletin of the American Mathematical Society, 2016. The brief of this paper is to explicate the origins, nature, and development of the second result, the discretized sum-product inequality, in analysis and beyond.
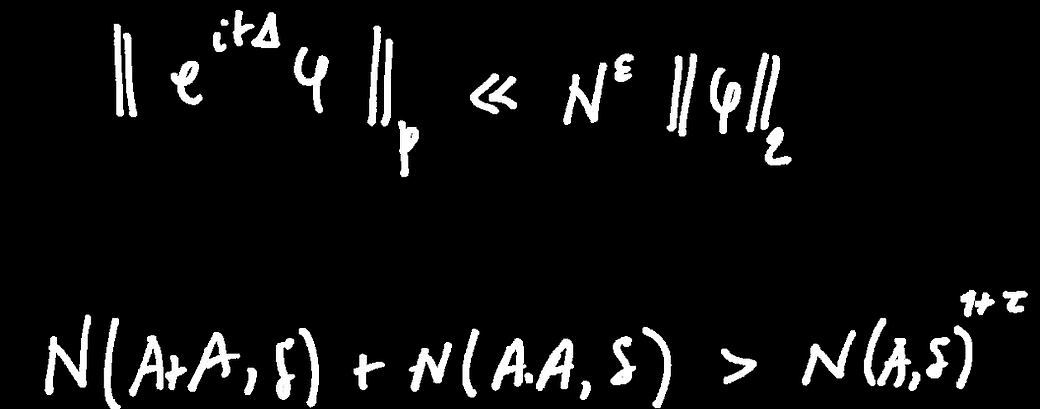
The three great branches of mathematics are, in historical order, Geometry, Algebra, and Analysis. Geometry we owe essentially to Greek civilization, algebra is of Indo-Arab origin, and analysis (or calculus) was the creation of Newton and Leibniz, ushering in the modern era. —Sir Michael Atiyah
Von Zahlen und Figuren — On Numbers and Shapes is the title of one of the most successful expositions of mathematics aimed at a broad audience, reflecting a common perception of our discipline as a marriage between algebra and geometry. This happy marriage, notwithstanding Count Tolstoy’s contention (“All happy marriages are alike; each unhappy marriage is unhappy in its own way.”), is not without tensions (as, perhaps, each happy marriage—including, possibly, bicameral mind—is in its own way). “In these days the angel of topology and the devil of abstract algebra fight for the soul of each individual mathematical domain” is the way Hermann Weyl put it in 1939.
This tension is embodied in the system of real numbers, the soil in which the functions of analysis grow, resembling Janus’s head facing in two directions: on the one hand, it is the field closed under the operations of addition and multiplication; on the other hand, it is a continuous manifold the parts of which are so connected as to defy exact isolation from each other. The one is algebraic, the other is the geometric face of real numbers. Continued fractions is a much more intrinsic and geometric form of discretizing the continuum; the lack of a practical algorithm for their addition and multiplication leads to the regnancy of the discretization based on the ordinary (digital or decimal, i.e., base 10) fractions.

Whereas Newton, in his development of calculus, was primarily motivated by “dynamics” (force, acceleration), as exemplified by the falling of the apple on his head, Leibniz, it appears, was more intrigued by what would now be described by the appellation fractal geometry of nature. “Imagine a circle; inscribe within it three other circles congruent to each other and of maximum radius; proceed similarly within each of these circles and within each interval between them, and imagine that the process continues ad infinitum,” wrote Leibniz referencing configuration akin to the four mutually tangent circles appearing on Baron Bourgain’s coat of arms. Leibniz’s definition of the straight line as a “curve, any part of which is similar to the whole, and it alone has this property, not only among curves but among sets” is a reflection of the fractal nature of the continuum: the Cantor set would satisfy Leibniz’s definition.1
Dynamics, broadly conceived, is perceived as a study of change, which in its primordial (physical) context takes place within time. The Cantor set (and the continuum) are time-less, i.e., static in time, but there is “a condition of possibility” of (almost) “equi-primordial” change “in the eye of the beholder,” taking form in changing the degree of magnification scale and “zooming in.” This is reflected in the “multi-scale” nature of Bourgain’s proof(s) of the discretized sum-product inequality.
To bring this opening section to a close, let us in passing note that both results chosen by Jean are not equalities (inequalities, rather), commenting thus:
If algebra is generally perceived as the study of equations, what perhaps lies at the heart of analysis are inequalities, or estimates, which compare the size of two quantities or expressions. Einstein’s discovery that nothing travels faster than light is an example of an inequality. The inequality 2X is considerably larger than X arguably neatly encapsulates both the P vs NP problem (properly stated for finite X) and Cantor’s continuum problem (when X is the first unfinite ordinal). An elementary inequality, taught in the middle school, asserts that the arithmetic mean of two positive numbers is never less than their geometric mean. In between these extremes, there is a vast range of estimates of great variety and importance. Such estimates, reflecting and quantifying some subtle aspect of the underlying problem, are often exceedingly difficult to prove. It will be seen that for the discretized sum-product inequality, with which we are about to get intimate, the underlying issue lies at the heart of the tension between the algebraic and (fractal)–geometric nature of the continuum. Fractal derives from Latin fractus, meaning broken apart; algebra, derives from the Arabic al-jabr, meaning the reunion of broken parts.
Origins: Kakeya-Besicovitch Problem
Hilbert’s democratic dictum, “Mathematical problem is not perfect unless you can explain it to the first man whom you meet on the street," if followed by Sōichi Kakeya (writing the paper on an island nation in 1917, at the height of the Great War), the explanation of the problem now bearing his name to almost every person on just about any street in Eastern Eurasia, might have run as follows: Entrusted with defending an island, possessing a huge hill, cragged and steep, your task is to purchase at the least cost to the nation’s treasury, a plot of land on the flat hilltop with the following property: a cannon of length one must be capable of pointing in any direction.
Kakeya improved by a factor of one-half the obvious solution (a circle of diameter one, having area π/4). His proposed shape was a three-cusped hypocycloid inscribed in the circle of radius 1. In the same year, working in Perm (subsequently Molotov, 1940–57; currently Perm), while the October/November Russian/Soviet Revolution was unfolding, A. S. Besicovitch reduced the minimal necessary sum to virtually nothing.
While the Kakeya set in the plane (two-dimensional space) has measure zero, it has fractal dimension 2 (see footnote 2). The basic conjecture is that in higher-dimensional spaces the same phenomenon holds: e.g., a set containing a line pointing in every direction in the three-dimensional space has fractal dimension 3. This conjecture, central to many problems in harmonic analysis, has been the subject of intense study by some of the most outstanding analysts of our time, with the major breakthrough by Bourgain in 1999, in which he related the Kakeya problem to arithmetic combinatorics.
Sum-product phenomena and the labyrinth of the continuum
One of the basic results in arithmetic combinatorics is the “sum-product phenomenon,” whose elementary and elemental nature might be described as follows. When studying addition and multiplication tables for numbers from 1 to 9, one might notice that there are many more numbers in the multiplication table. This basically has to do with the fact that the numbers from one to nine form an arithmetic progression. If you take a set forming an arithmetic progression (or a subset of it) and add it to itself, it will not grow much; if you take a set forming a geometric progression (or a subset of it) and multiply it by itself, it will also not grow much. However, a subset of integers cannot be both an arithmetic and a geometric progression, and so it will grow either when multiplied or added with itself. This is expressed as a statement |Α + Α | + |Α∙Α| ≥|Α|1+τ valid for any finite set of real numbers; here |Α| measures the size of the set, i.e., the number of elements in it.
Bourgain’s discretized sum-product inequality N (Α + Α, δ) + N (Α∙ Α, δ) > N (Α, δ)1+τ deals with infinite subsets of the continuum and measures their size in terms of “metric entropy” N (Α, δ), which is the least number of balls of diameter δ needed to cover Α. To oversimplify, the inequality says that for an arbitrary subset of the continuum, subject to mild technical assumptions, the fractal dimension would grow when it is multiplied or added to itself.
Discrete and Continuous Variations on the Expanding Theme
Expanders are highly connected sparse graphs widely used in computer science. Clearly high connectivity is desirable in any communication network. The necessity of sparsity is perhaps best seen in the case of the network of neurons in the brain: since the axons have finite thickness, their total length cannot exceed the quotient of the average volume of one’s head and the area of the axon’s cross-section. In fact, this is the context in which expander graphs first implicitly appeared in the work of Barzdin and Kolmogorov in 1967.
Now, there are basically two sources of raw material for constructing mathematical structures: randomness and number theory. It was observed early on that random regular graphs are expanders. The explicit construction of optimal expanders—Ramanujan graphs—used deep number–theoretic results from the theory of automorphic forms to construct expanders as Cayley graphs of groups3 with respect to some very special choices of generators.
A basic question that arose in 1994—at the time when I was starting my Ph.D.—is to what extent the expansion is the property of groups alone, independent of the choice of generators. I became fascinated/obsessed with this problem and obtained some partial results in my thesis under the direction of Peter Sarnak in 1999. In the fall of 2005, in joint work with Jean, we were able to finally resolve the problem in many cases by bringing in some recently developed tools from additive combinatorics, related to the sum-product phenomena.
These developments are discussed by Jean in his lecture "Expansion in Linear Groups and Applications"; see also: link.
Coda
In attempting to explain the significance of Bourgain’s remarkable and remarkably useful results to a proverbial human-on-line, one may invoke their applications in mathematical physics, computer science, and cryptography, which are of immense practical importance in contemporary life, making, in particular, the on-line communication possible. Their subtlety, beauty, and depth appear to be much harder to convey in “plain English.” Here and now, perhaps, we must remind ourselves that the human-on-line, while attached to a digital device (built by von Neumann) is still human and sound-bite/tweet thus: while dealing with entities seemingly fake/unreal (e.g., the real line), Bourgain’s singular adventures in the labyrinth of the continuum represent a magnificent and transcendent achievement of the human spirit.
I met Jean in September 2005, six months after my daughter was born, while visiting IAS for the program “Lie Groups, Representations and Discrete Mathematics,” led by Alex Lubotzky.4 I do not remember the precise date but do remember the hour: it was between 2 and 3 a.m. After changing my daughter’s diapers, I could not sleep, went to Simonyi Hall, and ran into Jean walking to the library. It was in this discombobulated state that I was free of fear to speak to him. By dawn, the problem which had been resisting my protracted attack for a decade was vanquished in Jean’s office.5
During this happiest year of my life, in 2005–06, I stayed on the lane named after Hermann Weyl who was of the view that “Mathematics in not the rigid and uninspiring schematism which the laymen is so apt to see in it; on the contrary, we stand in mathematics precisely at that point of limitation and freedom which is the essence of man himself.”
The seal of the IAS (where Jean did most of the work described in this essay) is a quiet, elegant, and classical Art Deco composition depicting two graceful young ladies, one clothed (Beauty) and one otherwise (Truth), standing on opposite sides of a leafy tree that appears to bear abundant fruit. Underlaying the design of the seal is the evident allusion to the famous final couplet of “Ode on a Grecian Urn” by John Keats, who was of the view that “the excellence of every art is its intensity, capable of making all disagreeables evaporate from their being in close relationship with Beauty and Truth.”
Having attempted in this essay a snapshot of the excellence of Bourgain’s art, let me conclude by giving a glimpse of his intensity by quoting from the interview upon his receiving the 2017 Breakthrough Prize in Mathematical Sciences:
If you have a question which is generally perceived as unapproachable, it is often that you do not even quite know where you have to look to get a solution. From that point of view, we are rather like Fourier stranded in the desert, hopelessly lost. At the moment you get this insight, all of a sudden you escape the desert and things open up for you. Then we feel very excited. These are the best moments. They make up for all the suffering with absolutely no progress worth it.
1. Leibniz also wrote the first textbook on combinatorics Dissertatio de arte combinatoria and invented the binary notation, which made possible modern computers and will play an important role in navigating the labyrinth of Bourgain’s argument. The first collection of Leibniz’s works was published in 1735 by Rudolf Erich Raspe, better known today for his authorship of Singular Adventures of Baron Munchausen.
2. If A is a curve, it is easy to see that N(A, δ) is of order δ-1. If A is a surface, N (A, δ) is approximately δ-2. This suggests the idea of defining the fractal dimension of an arbitrary set as the number d for which N(A, δ) ~ δ-d.
3. The Cayley graph of PSL2(Fp) for p = 5 with respect to standard generators is a buckyball.
4. https://mathinstitutes.org/highlights/expander-graphs
5. Jean had the following daily routine. He would arrive at the dining hall for lunch within 5 minutes of its closing and, while descending the stairs, would look for whom to join for the meal (the relevance of the person was determined primarily by their expertise in the problem Jean was currently working on). After lunch and before sunset, the door of his office would be half-open. After getting a bottle or red wine (typically Medoc), Jean would have dinner around 9 p.m., followed by a double espresso (typically at Small World Coffee), return to the office, call his wife and son, and then go for a brisk walk, encircling the Einstein Drive 5 times or so. Between midnight and sunrise, the office door would typically be closed. His handwritten notes (like that of Mozart’s and unlike Beethoven’s) are virtually free of corrections, in part, because during the dinner and the walk he would think about what would be set to paper upon his return to the office.