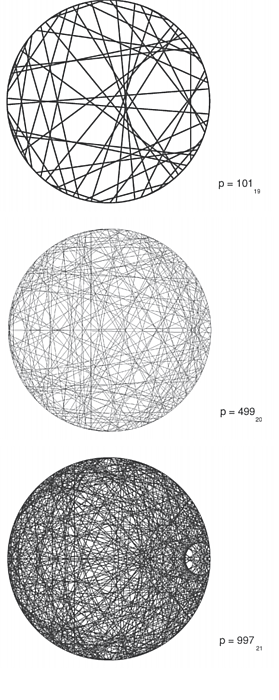
The study of expander graphs has been a rapidly developing subject in discrete mathematics and computer science. Expander graphs are sparse graphs, meaning they have few edges, with strong connectivity properties. They have many applications, including in efficient communication networks, derandomization, error-correcting codes, quantum computation, group theory, geometry, and number theory. In his seminar on expansion in linear groups and applications, Jean Bourgain discussed the existence of expander graph families and their construction. How much does the expansion property depend on the generators? Is expansion a property of the group? Recent advances have produced a robust theory of expander graphs for groups SL2 (p) based on arithmetic combinatorics.