Modular arithmetic has been a major concern of mathematicians for at least 250 years, and is still a very active topic of current research. In this article, I will explain what modular arithmetic is, illustrate why it is of importance for mathematicians, and discuss some recent breakthroughs.
For almost all its history, the study of modular arithmetic has been driven purely by its inherent beauty and by human curiosity. But in one of those strange pieces of serendipity which often characterize the advance of human knowledge, in the last half century modular arithmetic has found important applications in the “real world.” Today, the theory of modular arithmetic (e.g., Reed-Solomon error correcting codes) is the basis for the way DVDs store or satellites transmit large amounts of data without corrupting it. Moreover, the cryptographic codes which keep, for example, our banking transactions secure are also closely connected with the theory of modular arithmetic. You can visualize the usual arithmetic as operating on points strung out along the “number line.”
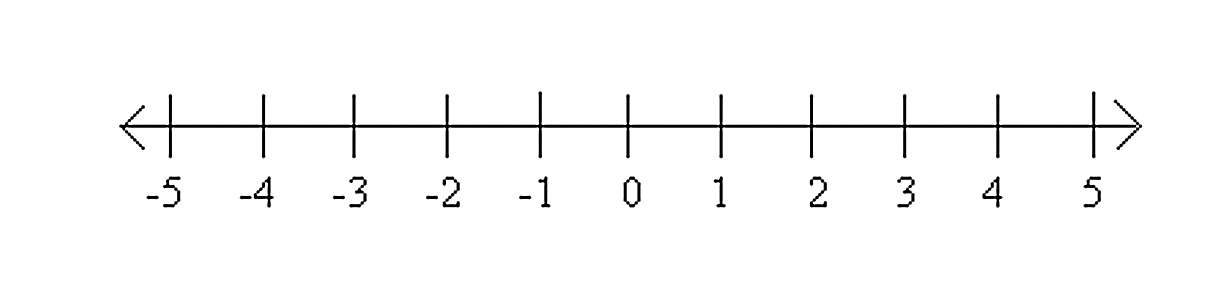
To add 3 and 5, you start at 0, count 3 to the right, and then a further 5 to the right, ending on 8. To multiply 3 by 5, you start at 0 and count 3 to the right 5 times ending up at 15. These sorts of operations should be familiar from elementary school.
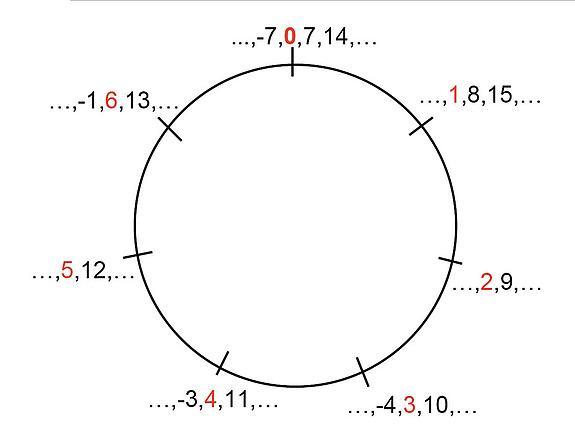
In modular arithmetic, one thinks of the whole numbers arranged around a circle, like the hours on a clock, instead of along an infinite straight line. One needs to decide at the outset how many “hours” our clock is going to have. It can be any number, not necessarily 12. As a first illustration, let’s suppose that we have seven “hours” on our clock—we say we are doing arithmetic modulo 7.
MODULO 7 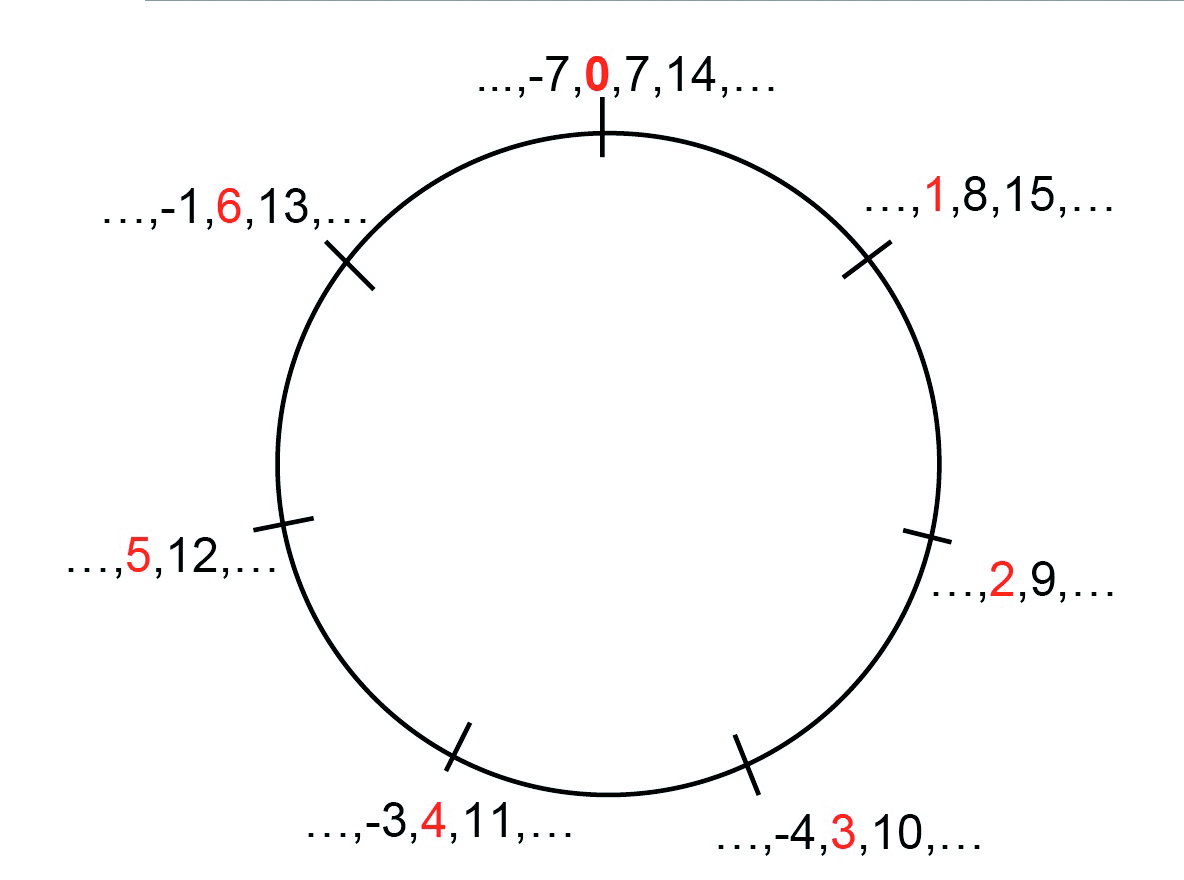
To add 3 and 5 modulo 7, you start at 0, count 3 clockwise, and then a further 5 clockwise, this time ending on 1. To multiply 3 by 5 modulo 7, you start at 0 and count 3 clockwise 5 times, again ending up at 1. We would write
3 + 5 ≡ 1 mod 7 and 3 × 5 ≡ 1 mod 7.
As we mentioned above, there is nothing special about 7. We can put any number of “hours” around our clock face and do arithmetic modulo any whole number. Our usual clocks can be used to do arithmetic modulo 12. If you go to a 2-hour movie starting at 11 o’clock, you will get out at 1 o’clock. This illustrates the following equality in arithmetic modulo 12:
11 + 2 ≡ 1 mod 12.
This may seem a rather trite variant on our usual arithmetic, and the reader could legitimately wonder if it is more than a curiosity. I hope this article will convince her that it is.
An important observation is that any arithmetic equality that is true in normal arithmetic is also true in modular arithmetic modulo any whole number you like. This easily results from the observation that one can wind the usual number line around the modular clock face, turning usual arithmetic into modular arithmetic.
______________
To illustrate a major reason why mathematicians care about modular arithmetic, let me start with one of the oldest questions in mathematics: Find Pythagorean triples, i.e., find whole number solutions, to the equation
X 2 + Y 2 = Z 2.
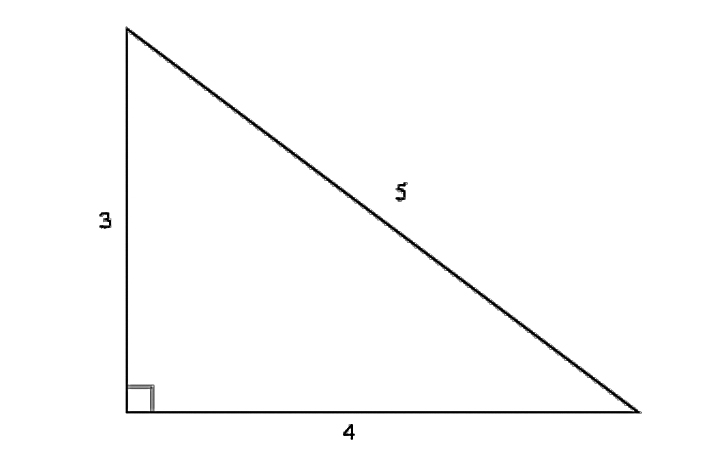
By Pythagoras’s theorem, this is the same as finding right-angled triangles all of whose sides have lengths that are whole numbers (when measured in the same units). For instance
32 + 42 = 52
and there is a right-angled triangle:
The 3,800-year-old Babylonian tablet Plimpton 322 lists Pythagorean triples. The second column of the tablet lists values for X and the third column the corresponding value of Z; the value of Y is not listed.

In modern notation, the solutions listed on Plimpton 322 are as follows:
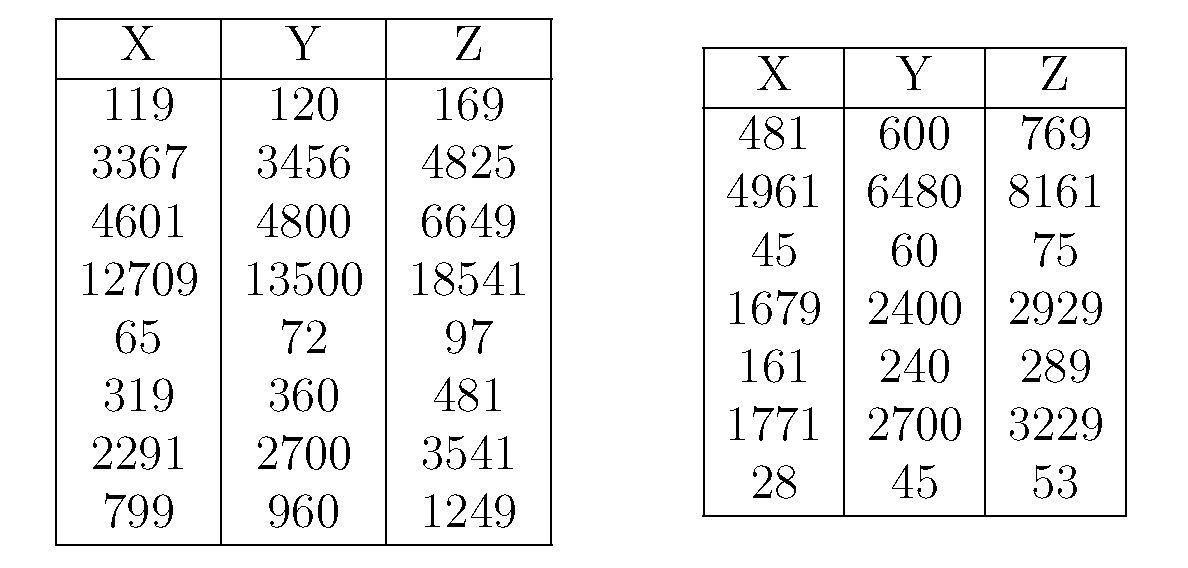
It is noteworthy that some of these solutions are quite complicated, but we don’t know how they were generated. Could it have been trial and error, or did the Babylonians know an algorithm?
What is certain is that 1,500 years later the Greeks knew the algorithm to generate all whole number solutions to this equation. We know this because Euclid explained the method in Book X of his famous Elements. In modern algebraic notation, Euclid proves that every whole number solution to X 2 + Y 2 = Z 2 has the form
X = (a2 – b2)c/2 Y = abc Z = (a2 + b2)c/2
where a, b, and c are themselves whole numbers such that a, b, and c have the same parity (i.e., are both odd or both even).
But what if we change the problem slightly? What about asking for the solution of
X 2 + Y 2 = 2Z 2
or
X 2 + Y 2 = 3Z 2
in whole numbers? It turns out that as soon as we find one non-zero solution in whole numbers, the method described in Euclid’s Elements applies, and we can describe all solutions in whole numbers explicitly. So for instance the equation
X 2 + Y 2 = 2Z 2
has a solution
X = 1 Y = 1 Z = 1
and one deduces that the general point with whole number coordinates is of the form
X = (a2 + 2ab – b2 )c/2
Y = (–a2 + 2ab + b2)c/2 Z = (a2 + b2)c/2
where a, b, and c are themselves whole numbers such that a, b, and c have the same parity.
However, if you search for non-zero whole number solutions to X 2 + Y 2 = 3Z 2, you won’t find any. What is the difference between X 2 + Y 2 = Z 2 or X 2 + Y 2 = 2Z 2, and X 2 + Y 2 = 3Z 2? The answer comes from modular arithmetic.
Suppose there was a solution to
X 2 + Y 2 = 3Z 2,
with X, Y, and Z non-zero whole numbers. We can arrange that no whole number bigger than 1 divides all of X, Y, and Z. (If it did, simply divide each of X, Y, and Z by this common factor, and they still form a solution to the same equation. If need be, we repeat this process. Note that as the numbers X, Y, and Z get smaller in absolute value each time, but remain whole numbers, this procedure must eventually stop.) Then there would be a solution to the same equation in arithmetic modulo 3. But in arithmetic modulo 3 we have
3 × Z 2 ≡ 0 × Z 2 ≡ 0 mod 3
and
02 ≡ 0 and 12 ≡ 1 and 22 ≡ 1 mod 3,
i.e.,
X 2 ≡ 0 or 1 mod 3 and Y 2 ≡ 0 or 1 mod 3.
The only way we can have
X 2 + Y 2 ≡ 0 mod 3
is to have X 2 ≡ Y 2 ≡ 0 mod 3. This means that 3 divides X and Y; so that 9 divides X 2 + Y 2 = 3Z 2 ; so that 3 divides Z 2 ; so that 3 also divides Z . This is impossible, because we had arranged that no whole number greater than 1 divided each of X , Y , and Z . As we have reached a contradiction, the only possibility is that our initial assumption was flawed, i.e., there could not have been a solution to
X 2 + Y 2 = 3Z 2,
with X , Y, and Z non-zero whole numbers.
This sort of argument works not only for this particular equation. A beautiful theorem of Hermann Minkowski (1890) and Helmut Hasse (1924) says that if Q (X1 , ..., Xd ) is any homogeneous quadratic polynomial in any number of variables with whole number coefficients, then
Q (X 1, ..., X d) = 0
has a non-zero solution in whole numbers if and only if it has a non-zero solution in all (real) numbers and a primitive solution modulo m for all positive whole numbers m. (We call (X1 , ..., Xd ) a primitive solution modulo m if
Q (X 1, ..., X d ) ≡ 0 mod m,
but no integer greater than 1 divides all the Xi .) This is actually a very practical criterion. It may appear that one needs to check for solutions to our equation in arithmetic modulo m for infinitely many m. However, one can find a single integer m0 (which depends on the polynomial Q) with the property that, if Q (X1 , ..., Xd) = 0 has a primitive solution modulo m0, then it also has a primitive solution modulo m for any other positive whole number m.
However, for higher degree equations, the corresponding theorem can fail. For instance
3X 3 + 4Y 3 + 5Z 3 = 0
has non-zero solutions modulo every positive whole number (and it has a solution in the real numbers), but it has no non-zero solution in whole numbers. (This famous example was found by Ernst Selmer, former IAS Member.) Nevertheless, when studying the whole number solutions to any polynomial equation, the study of solutions modulo m is often a key tool.
______________
More than 1,800 years ago the Chinese text Sun Zi Suan Jing contained a statement of what is now referred to as the Chinese Remainder Theorem. This theorem gives a very efficient algorithm that reduces the study of the solutions to a polynomial equation in arithmetic modulo a whole number m, to the study of the same equation in arithmetic modulo the factors of m of the form pa, where p is a prime number and a is a positive whole number. In fact, it turns out that the key case to consider is when m is a prime number. Thus, for the rest of this article, we will only consider arithmetic modulo a prime number p.
Recall that a prime number is a whole number greater than 1, which is only divisible by 1 and by itself. Examples are 2, 3, 5, 7, 11, 13, 17, and 19, but not for instance 15, which is divisible by 3 and 5. Every positive whole number can be written uniquely as a product of prime numbers (up to order). In some way, prime numbers are a bit like the atoms of which all other whole numbers are composed.
The first really great achievement in the study of modular arithmetic was Carl Friedrich Gauss’s proof in 1796 of his celebrated law of quadratic reciprocity, which had previously been conjectured by Leonhard Euler and Joseph Lagrange. This was supposed to have been Gauss’s favorite theorem, and he kept coming back to it during his life, giving eight different proofs. It states that
if p is a prime number, then the number of square roots of an integer n in arithmetic modulo p depends only on p modulo 4n.
On the face of it, this may not seem surprising, but I would stress that there is no apparent reason why trying to solve the equation
X 2 ≡ n mod p
should have anything to do with p modulo 4n. Thirty years after I first learnt how to prove this theorem, it still seems miraculous to me.
Gauss’s theorem also provides a very effective way of determining the number of square roots a whole number has in arithmetic modulo a prime number p. For example, one could ask how many square roots 3 has in arithmetic modulo 20132011, which is a prime number. You could, in theory, check all the 20132011 possibilities and determine the answer, but (without a computer) this would take a very long time. On the other hand
20132011 = 1677667 × 12 + 7
so that 3 has the same number of square roots in arithmetic modulo 20132011 as it does in arithmetic modulo 7. But it is very quick to list the squares modulo 7:
02 ≡ 0, 12 ≡ 1, 22 ≡ 4, 32 ≡ 2, 42 ≡ 2, 52 ≡ 4, 62 ≡ 1 mod 7.
Thus 3 has no square root in arithmetic modulo 7 and so by Gauss’s theorem it has no square root in arithmetic modulo 20132011. (A good thing we didn’t waste our time checking all 20132011 possibilities!)
One could ask for a similar method that given any number of polynomials in any number of variables helps one to determine the number of solutions to those equations in arithmetic modulo a variable prime number p. Such results are referred to as “reciprocity laws.” In the 1920s, Emil Artin gave what was then thought to be the most general reciprocity law possible—his abelian reciprocity law. However, Artin’s reciprocity still only applied to very special equations—equations with only one variable that have “abelian Galois group.”
Stunningly, in 1954, Martin Eichler (former IAS Member) found a totally new reciprocity law, not included in Artin’s theorem. (Such reciprocity laws are often referred to as non-abelian.) More specifically, he found a reciprocality law for the two variable equation
Y 2 + Y = X 3 – X 2.
He showed that the number of solutions to this equation in arithmetic modulo a prime number p differs from p by the coefficient of q p in the formal (infinite) product
q(1 – q) 2 (1 – q11) 2 (1 – q 2) 2 (1 – q 22 ) 2 (1 – q 3) 2 (1 – q 33) 2 (1 – q4) 2 ... = q – 2q 2 – q 3 + 2q 4 + q 5 + 2q 6 – 2q 7 – 2q 9 – 2q 10 + q 11 – 2q 12 + . . .
For example, you see that the coefficient of q 5 is 1, so Eichler’s theorem tells us that
Y 2 + Y = X 3 − X 2
should have 5 − 1 = 4 solutions in arithmetic modulo 5. You can check this by checking the twenty-five possibilities for (X,Y) modulo 5, and indeed you will find exactly four solutions:
(X,Y) ≡ (0,0), (0,4), (1,0), (1,4) mod 5.
Within less than three years, Yutaka Taniyama and Goro Shimura (former IAS Member) proposed a daring generalization of Eichler’s reciprocity law to all cubic equations in two variables. A decade later, André Weil (former IAS Professor) added precision to this conjecture, and found strong heuristic evidence supporting the Shimura-Taniyama reciprocity law. This conjecture completely changed the development of number theory.
In the mid-1980s, Gerhard Frey, Jean-Pierre Serre (former IAS Member), and Kenneth Ribet (former IAS Member) showed that the Shimura-Taniyama reciprocity law, if true, would imply Fermat’s Last Theorem. Motivated by this, in 1995, Andrew Wiles (former IAS Member), partly in collaboration with the author, established many cases of the Shimura-Taniyama reciprocity law and hence finally proved Fermat’s Last Theorem.
Meanwhile, in the mid-1970s, Robert Langlands (Professor Emeritus, School of Mathematics) had the extraordinary insight that the ideas of Eichler, Taniyama, and Shimura were a small part of a much bigger picture. He was able to conjecture the ultimate reciprocity law, an enormous generalization of what had gone before, which applies to any number of equations, of any degree in any number of variables. In the last ten years, using the ideas introduced by Wiles, there has been much progress made on Langlands’s reciprocity conjecture, but much more still remains to be done.
One striking feature of all the non-abelian reciprocity laws is that the formula for the number of solutions is given in terms of symmetries of certain curved spaces—an extraordinary connection between solving algebraic equations and geometric symmetry. In the case of the Shimura-Taniyama reciprocity law, the relevant symmetries are those of the “hyperbolic plane.” The hyperbolic plane can be thought of as a circular disc (without its boundary), but with an unusual notion of distance. For two points near the center of the disc, their “hyperbolic” distance is similar to their usual distance, but distances are increasingly distorted near the edge of the disc. The hyperbolic plane and its symmetries were illustrated in some of Escher’s woodcuts, like the one below. In the hyperbolic world, all the fish in Escher’s print are to be thought of as having the same size.
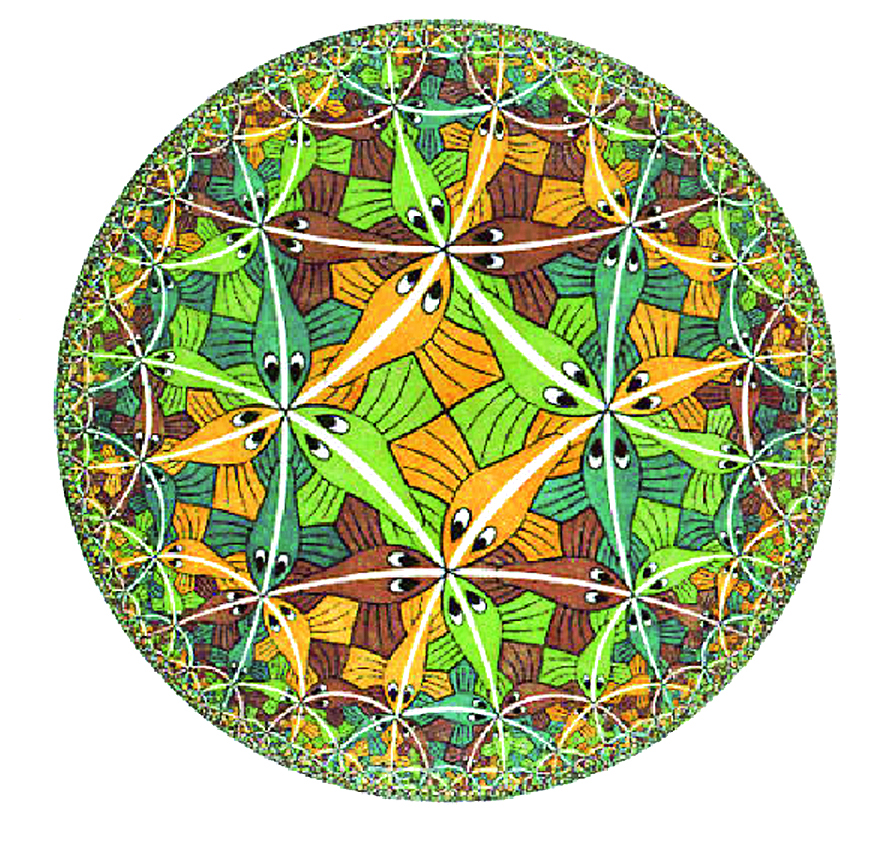
Circle Limit III M. C. Escher
______________
I will conclude by discussing one further question about modular arithmetic which has seen recent progress.
Instead of asking for a rule to predict how many solutions an equation will have in arithmetic modulo a varying prime p, one can ask about the statistical behavior of the number of solutions as the prime varies. Going back to the simple case of a quadratic equation in one variable, Lejeune Dirichlet showed in 1837 that for a fixed whole number m, which is not a prefect square, the equation
X 2 ≡ m mod p
has two solutions for half of all prime numbers p and no solutions for half of all prime numbers p. This may seem a natural answer, but Dirichlet’s proof was very subtle, combining Gauss’s reciprocity law with ideas from complex analysis. In 1880, Ferdinand Frobenius generalized Dirichlet’s theorem to any equation in one variable.
For other equations, the correct answer may be harder to guess. For instance, the equation
X 4 ≡ 2 mod p
has no solution for 5/8 of all prime numbers p; has two solutions for 1/4 of all prime numbers p; and has four solutions for 1/8 of all prime numbers p.
What about such density theorems for equations in more than one variable, like
Y 2 + Y = X 3 − X 2?
In this case, Hasse showed in 1933 that the number of solutions in arithmetic modulo p, which we will denote Np , is of the same order of magnitude as p. More precisely, he showed that Np differed from p by at most 2√p . He proved this for all cubic equations in two variables.
In 1949, Weil conjectured an enormous generalization of Hasse’s bound to any number of equations in any number of variables of any degree. These celebrated conjectures led to a revolution in arithmetic algebraic geometry. Weil’s conjectures were finally proved by Pierre Deligne (Professor Emeritus, School of Mathematics) in 1974.
Returning to the equation
Y 2 + Y = X 3 − X 2,
Hasse’s theorem tells us that asking for what fraction of primes this equation has—say, ten solutions in arithmetic modulo p—is not interesting; the answer will always be 0. Rather the natural question is to consider the normalized error term
Np − p
—
√p.
By Hasse’s theorem, this will be a (real) number lying between −2 and 2, and one can ask how it is distributed in this interval. Is the error often as large as Hasse’s theorem allows, or is it usually smaller and only rarely at the extreme? In 1963, Mikio Sato and John Tate (both former IAS Members) independently conjectured the correct density theorem—the error should be distributed like (1/2π) √4 − t 2, a “squashed semi-circle.”
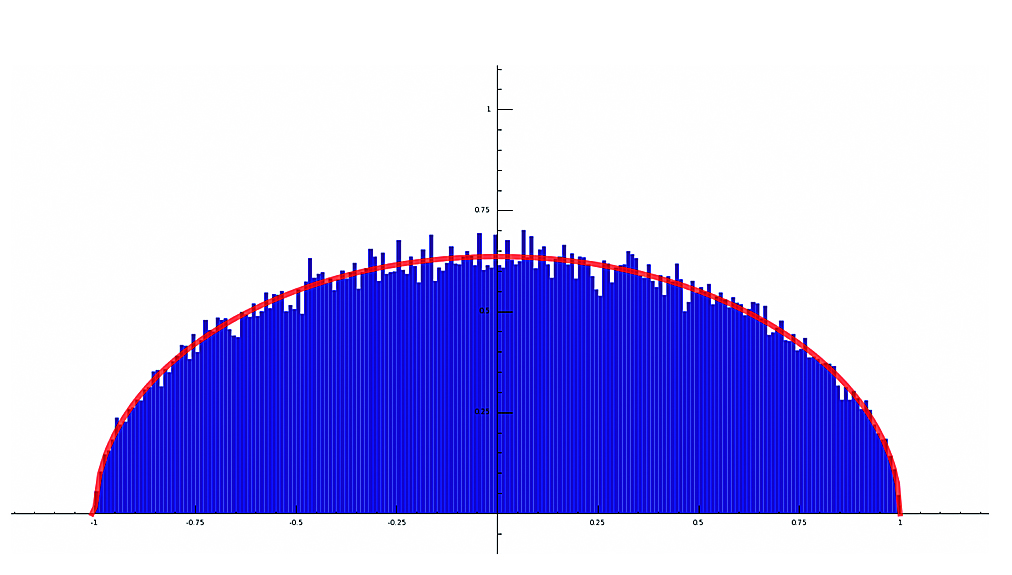
Sato-Tate Distribution for Δ and p <1,000,000
(drawn by William Stein)
The Sato-Tate density theorem has recently been proven (by Laurent Clozel and Michael Harris, both former IAS Members; Nicholas Shepherd-Barron; and the author), not just for this equation, but for all cubic equations in two variables. The proof combines the arguments of Dirichlet and Frobenius with an infinite series of new cases of Langlands’s reciprocity law. There should, of course, be density theorems for any number of equations in any number of variables of any degree, but these remain very much conjectural. The story is continuing . . .