The Fundamental Lemma: From Minor Irritant to Central Problem
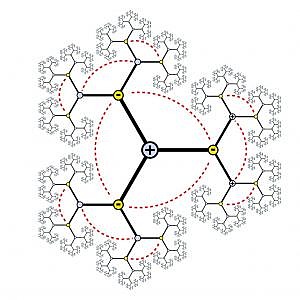
The proof of the fundamental lemma by Bao Châu Ngô that was confirmed last fall is based on the work of many mathematicians associated with the Institute for Advanced Study over the past thirty years. The fundamental lemma, a technical device that links automorphic representations of different groups, was formulated by Robert Langlands, Professor Emeritus in the School of Mathematics, and came out of a set of overarching and interconnected conjectures that link number theory and representation theory, collectively known as the Langlands program. The proof of the fundamental lemma, which resisted all attempts for nearly three decades, firmly establishes many theorems that had assumed it and paves the way for progress in understanding underlying mathematical structures and possible connections to physics.
The simplest case of the fundamental lemma counts points with alternating signs at various distances from the center of a certain tree-like structure. As depicted in the above image by former Member William Casselman, it counts 1, 1–3=–2, 1–3+6=4, 1–3+6–12=–8, etc. But this case is deceptively simple, and Ngô’s final proof required a huge range of sophisticated mathematical tools. The story of the fundamental lemma, its proof, and the deep insights it provides into diverse fields from number theory and algebraic geometry to theoretical physics is a striking example of how mathematicians work at the Institute and demonstrates a belief in the unity of mathematics that extends back to Hermann Weyl, one of the first Professors at the Institute. This interdisciplinary tradition has changed the course of the subject, leading to profound discoveries in many different mathematical fields, and forms the basis of the School’s interaction with the School of Natural Sciences, which has led to the use of ideas from physics, such as gauge fields and strings, in solving problems in geometry and topology and the use of ideas from algebraic and differential geometry in theoretical physics.
It also poignantly underscores the Institute’s continual commitment to the philosophy of Abraham Flexner, founding Director of the Institute, who argued the case for curiosity-driven rather than objective-driven research and emphasized the “usefulness of useless knowledge.” It was his belief that if the Institute “eschews the chase for the useful, the minds of its scholars will be liberated, they will be free to take advantage of surprises, and someday an unexpected discovery, apparently leading now here, will be found to be an indispensable link in a long and complex chain that may open new worlds in theory and practice.”
The fundamental lemma has been described as a gross understatement.1 “The curious thing is that it is called a lemma [a subsidiary proposition to be proved on the way to demonstrating a principal proposition]. It is a theorem,” says Andrew Wiles, a Visitor in the School of Mathematics and an Institute Trustee. “At first, it was thought to be a minor irritant, but it subsequently became clear that it was not a lemma but rather a central problem in the field.”
Robert Langlands, Professor Emeritus in the School of Mathematics, first introduced the fundamental lemma in 1979 in a lecture, “Les débuts d’une formule des traces stable,” at the École Normale Supérieure de Jeunes Filles and published in Publications Mathématiques de l’Université Paris VII.2 The goal of the lecture was the stabilization of the Selberg trace formula, but it also introduced the fundamental lemma, a technical device that links automorphic representations of different groups and the notion of closely related transfer factors that could transport automorphic forms. This led to the creation of a field of study that Diana Shelstad, a former Member in the School of Mathematics and Langlands’s student, eventually called “endoscopy.”
In the theory of endoscopy, the Selberg trace formula (introduced by the late Atle Selberg, Professor in the School of Mathematics) is used to distinguish the internal structure of automorphic representations of different groups. The fundamental lemma, which has been described as a matching conjecture,3 is a very precise conjecture used in the Selberg trace formula to prove some cases of the principle of functoriality. The principle of functoriality is a core conjecture of the Langlands program that seeks to establish symmetry between whole numbers and links automorphic representations of different groups through their L-groups. Using layman’s terms, Peter Sarnak, Professor in the School of Mathematics, compares the fundamental lemma to a screwdriver, functoriality to opening a screw, and the Langlands program to the big machine working to reveal the underlying structure of automorphic forms.
Over the years, the fundamental lemma turned out to be incredibly difficult to prove in the general case, although progress was made in specific cases, through work done by Langlands, his students, and others at the Institute and elsewhere. For more than two decades, Langlands gave up on resolving the fundamental lemma and spent his time studying fields unrelated to the Langlands program, most recently lattice models of statistical physics and the attendant conformal invariance. “The fundamental lemma was a problem that I thought was easy and it turned out to be hard,” says Langlands. “The impulse is to concentrate on the problem, and so you concentrate on it for years. You don’t, for obvious reasons, have the confidence to think beyond it. You can say, ‘Well, I’ll just assume it and think beyond it.’ But then every person you meet will say, ‘But what if it isn’t true?’”
Still, the resolution of the fundamental lemma was presumed in major works, such as the stabilization of the Arthur-Selberg trace formula. (The Arthur-Selberg trace formula itself was developed by James Arthur, a former Member and Trustee.) Last fall, thirty years after Langlands first introduced it, a proof of the fundamental lemma by Bao Châu Ngô, a Member in the School of Mathematics from 2006–10, was confirmed. (Financial support for Ngô’s Membership in 2009–10 was provided by the Charles Simonyi Endowment and the Ambrose Monell Foundation.)
Ngô’s proof, based on a geometric interpretation of endoscopy theory, follows the work of many other mathematicians, including Mark Goresky, Thomas Hales, Hervé Michel Jacquet, Robert Kottwitz, Jean-Pierre Labesse, Gérard Laumon, Robert MacPherson, Jonathan Rogawski, Shelstad, Rainer Weissauer, and Jean-Loup Waldspurger. “It is very rare that you can take a proof in the geometric setting and convert it to the genuine number theoretic setting. That is what has transpired through Ngô’s achievement,” says Sarnak. “Ngô has provided a bridge, and now everybody is using this bridge. What he has done is deep. It is below the surface and it is understanding something truly fundamental. There are a number of theorems that, in the past, would have included the statement, ‘Assume the fundamental lemma, then the following remarkable thing is true.’ A number of theories—statements that were of great interest but weren’t known to be true––are now known to be true.”
In 1967, Langlands wrote a seventeen-page handwritten letter to André Weil, a Professor at the Institute at the time, in which he proposed a grand unifying theory that relates seemingly unrelated concepts in number theory, algebraic geometry, and the theory of automorphic forms. A typed copy of the letter,4 made at Weil’s request for easier reading, circulated widely among mathematicians in the late 1960s and 1970s, and for more than three decades, mathematicians have been working on its conjectures, known collectively as the Langlands program.
The Langlands program, of which endoscopy theory is a part, is incredibly vast and far-reaching and has many different manifestations. “It is one of the great insights into twentieth-century mathematics. It is a beautiful synthesis of the theory of numbers and symmetry—the theory of groups—specifically Lie groups, ” says Sarnak. “It gives a vision of what you can do with a theory of groups in connection with number theory. It gives the boundaries of what you can hope to do, but it also shows what you can’t do. This insight has created fruits in every direction, meaning people who work on some little aspect of it are forced to understand what they’re doing better in order that other people can use it.”
In addition to changing the field of automorphic forms drastically, making the infinite-dimensional representation theory of reductive groups into a major field of mathematical activity, and introducing a general class of L-functions that have had major consequences for algebraic number theory, Langlands’s conjectures have had a significant influence on other fields, such as physics. In the geometric Langlands program, created by former Member Vladimir Drinfeld and collaborators, some of the ideas are converted from number theory into statements in geometry. The geometric form is particularly rich for implications in theoretical physics, especially string theory. In 2006, Edward Witten, Charles Simonyi Professor in the School of Natural Sciences, cowrote a 225-page paper on the relation of part of the geometric Langlands program to ideas of the duality between electricity and magnetism.5 During his time at the Institute, Ngô has been working on a program to bring the Arthur-Selberg trace formula into the framework of the geometric Langlands program.
The use of the trace formula to prove cases of functoriality requires combinatorial identities—the fundamental lemma—between orbital integrals. Orbital integrals and weighted orbital integrals are the basis of the local harmonic analysis and invariant harmonic analysis theories developed by the late Harish-Chandra, Professor in the School of Mathematics. “In crude terms, one side of the trace formula contains terms related
to the characters of automorphic representations,” observes Hales.6 “The other side contains terms such as orbital integrals. Thanks to the trace formula, identities between orbital integrals on different groups imply identities between the representations of the two groups.”
From early on, attempts to prove the fundamental lemma have involved geometric interpretations of the identities of orbital integrals––interpretations that have become increasingly sophisticated through the work of Goresky, Kottwitz, Laumon, MacPherson, and Ngô.
Ngô’s interest in the fundamental lemma7 came in the late 1990s when he was writing his Ph.D. dissertation on a conjecture related to the fundamental lemma by Jacquet (who, with Langlands, proved the Jacquet-Langlands correspondence in 1970, providing one of the first examples of functoriality8). “Through my work on Jacquet’s conjectures, I found a completely new method to tackle these kinds of problems to prove equalities,” says Ngô. “I was quite tempted by Langlands’s fundamental lemma but I was ill equipped. I needed to learn more of the mathematics and understand what it was about. I did not work on the lemma for maybe five or six years until I felt ready. In the meantime, other people were working on it. My own ideas were certainly not enough.”
By 2004, Ngô was deeply invested in trying to solve the fundamental lemma. But he ran into a roadblock while trying to use the equivariant cohomology approach, which provides essential insight into the topological nature of the lemma, introduced by Goresky, Kottwitz, and MacPherson, Hermann Weyl Professor in the School of Mathematics. “I went into quite a despair. I had spent three years working on every possible angle,” says Ngô. “I still believed the problem I set for myself was a good one. But I was missing one step.” In 2006, during a three-month visit to the Institute, where he conducted a seminar on the fundamental lemma, Ngô asked Goresky about a statement concerning perverse sheaves, which is unrelated to the fundamental lemma but provided insight for Ngô. “He explained to me one example that he and MacPherson knew where it could be proved,” says Ngô. “It was the missing piece of my puzzle. Everything fit together. Still, it was not an easy process. There were a lot of details that had to be worked out very carefully.” By spring 2007, Ngô was convinced that his proof worked. He returned to the Institute in fall 2007 and ran another seminar about the fundamental lemma, during which his proof was scrutinized by Pierre Deligne, Professor Emeritus in the School of Mathematics, and others. His paper went through six different versions before it was made available online in 2008, and recently published.9
It was Waldspurger’s work that suggested that the proof of the fundamental lemma could be arrived at in the geometric setting, which allows deformations, in contrast to number theory, which does not. Transfer factors, wherein orbital integrals on one group are multiplied in order to be orbital integrals on the other, are necessary to transport automorphic forms. A transfer conjecture was formulated initially by Langlands and Shelstad, then later by Kottwitz and Shelstad in a more flexible and twisted form. In the mid 1990s, Waldspurger proved that the transfer conjecture would follow from the corresponding fundamental lemma.
“This was quite a surprise,” notes Arthur.10 “For the fundamental lemma pertains to very special functions at certain p-adic places, while the transfer conjecture applies to general functions at all p-adic places. Waldspurger used global methods, specifically a simple version of the trace formula, to solve what was a local problem.” Shelstad had already solved the transfer problem for archimedian places, using Harish-Chandra’s work, which served as a guide for the construction of general transfer factors. In the past few years, Waldspurger also completed a far-reaching study in harmonic analysis, which among other things reduces the transfer conjecture of Kottwitz and Shelstad to a form of the fundamental lemma.
In his proof of the fundamental lemma, Ngô exploited the interplay of local and global methods in “ingenious ways,” according to Arthur, and “observed that the entire geometric side could be expressed as a sum over the rational points of an arithmetic Hitchin fibration, the arithmetic analogue of a variety familiar from the theory of G-bundles on a Riemann surface.”
Important arithmetic applications follow from endoscopy theory, including the transfer of automorphic representations from classical groups to linear groups and the construction of Galois representations attached to automorphic forms via Shimura varieties (developed by Goro Shimura, a frequent Member at the Institute). Shimura varieties are a central part of Langlands’s program, both as a source of representations of Galois groups and as tests for the conjecture that all motivic L-functions are automorphic.11 In addition to being critical to the comparison of trace formulas that is part of the theory of endoscopy, the fundamental lemma is essential in the comparison of the automorphic Arthur-Selberg trace formula and the geometric Grothendieck-Lefschetz trace formula needed to establish reciprocity laws for Shimura varieties.
With the proof of the fundamental lemma, Langlands is thinking again about how the stabilized trace formula might be used to establish the basic conjectures he outlined in 1967. “Until recently, I didn’t have any idea how one could attack these basic conjectures in a genuinely promising fashion,” says Langlands. “But thinking about the proof of the fundamental lemma and the techniques it provides, I shouldn’t say I’m optimistic, but I really think there is something there on which one can get a handle.”
About six years ago, when he heard of the progress being made with the fundamental lemma, Langlands began working in an area he calls “beyond endoscopy.” Primary among Langlands’s interests is using the Arthur-Selberg trace formula to resolve the principle of functoriality beyond endoscopy, which only analyzes representations of G in terms of representations of its endoscopic groups. For Langlands, it is not the fundamental lemma that is critical for the analytic theory of automorphic forms and for the arithmetic of Shimura varieties; it is the stabilized (or stable) automorphic trace formula that the fundamental lemma now establishes, namely, the reduction of the Arthur-Selberg trace formula to a stable trace formula for a group and its endoscopic groups, as well as the stabilization of the geometric Grothendieck-Lefschetz trace formula. “None of these are possible without the fundamental lemma, and its absence rendered progress almost impossible for more than twenty years,” comments Langlands. “I hope that with the fundamental lemma at hand we will see in the coming years great progress both with functoriality and with the general theory of Shimura varieties.”
In the past year, Langlands and Ngô wrote a paper with former Member Edward Frenkel (to be published in Annales des sciences mathématiques du Québec) in which the stable trace formula allows the introduction of the Steinberg-Hitchin base and of the Poisson summation formula.12 They observe a close relationship between the trace formula and Beilinson-Drinfeld’s conjecture in the geometric Langlands program. In a related work,13 Frenkel and Witten have used the mirror symmetry of the Hitchin fibrations to expose the special role played by endoscopy in the geometric Langlands correspondence. This correspondence has been interpreted as the mirror symmetry of the Hitchin fibrations for two dual reductive groups.
Speaking of Ngô’s geometric interpretation of the identities of orbital integrals for his proof of the lemma, Langlands says, “I am only very, very slowly coming to appreciate that Ngô’s point of view on orbital integrals might supplement in important ways, maybe even replace, that of Harish-Chandra’s. Certainly, it will be important for many other matters connected with invariant harmonic analysis, not just the fundamental lemma. From a technical point of view, I think that Ngô’s work offers tools that Harish-Chandra didn’t have, and they would have been a big help to him. I think it would have helped him see many things more clearly.”
1 Preface by James Arthur, David Ellwood, Robert Kottwitz in Harmonic Analysis, the Trace Formula, and Shimura Varieties, Clay Mathematics Proceedings 4 (2005), 265–66, www.claymath.org/library/proceedings/cmip04.pdf
2 http://publications.ias.edu/rpl_works/L8/debuts/traces-ps.pdf
3 www.mfo.de/programme/prize/Ngo2008.pdf
4 http://publications.ias.edu/rpl/comments.php?paper=313
5 “Electric-Magnetic Duality and the Geometric Langlands Program,” by Anton Kapustin and Edward Witten, http://arxiv.org/abs/hep-th/0604151v3
6 “A Statement of the Fundamental Lemma,” by Thomas C. Hales in Harmonic Analysis, the Trace Formula, and Shimura Varieties, Clay Mathematics Proceedings 4 (2005), 651, www.claymath.org/library/proceedings/cmip04.pdf
7 “Report on the Fundamental Lemma,” by Bao Châu Ngô, www.math.ias.edu/~ngo/cdm.pdf
8 http://publications.ias.edu/rpl/series.php?series=52
9 “Le lemme fondamental pour les algèbres de Lie,” by Bao Châu Ngô, Publications Mathématiques de l’IHÉS 111 (2010), 1–169, www.springerlink.com/content/h745w76118173910
10 “Transfer, the Fundamental Lemma, and the Work of Waldspurger," by James Arthur, Clay Mathematics Institute Annual Report 2009, 7–9
11 “Introduction to Shimura Varieties,” by J. S. Milne in Harmonic Analysis, the Trace Formula, and Shimura Varieties, Clay Mathematics Proceedings 4 (2005), 265–66, www.claymath.org/library/proceedings/cmip04.pdf
12 “Formule des Traces et Fonctorialité: le Début d’un Programme,” by Edward Frenkel, Robert Langlands, and Bao Châu Ngô, http://arxiv.org/abs/1003.4578v1
13 “Geometric Endoscopy and Mirror Symmetry,” by Edward Frenkel and Edward Witten, Communications in Number Theory and Physics 2, no. 1 (2008), 113–283, http://arxiv.org/pdf/0710.5939


