Pierre Deligne

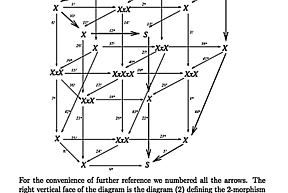
Pierre Deligne, Professor Emeritus in the School of Mathematics, joined the Institute Faculty in 1981. Deligne’s research pursues a fundamental understanding of the basic objects of arithmetical algebraic geometry—motive, L-functions, Shimura varieties—and applies the methods of algebraic geometry to trigonometrical sums, linear differential equations and their monodromy, representations of finite groups, and quantization deformation. A Fields Medalist for solving three Weil conjectures concerning generalizations of the Riemann hypothesis to finite fields, Deligne has done much to unify algebraic geometry and algebraic number theory.

Mathematics

The Fundamental Lemma

Kelly Devine Thomas
The Institute Letter Summer 2010

The fundamental lemma has been described as a gross understatement. Says Andrew Wiles, a Visitor in the School of Mathematics and an Institute Trustee, “At first, it was thought to be a minor irritant, but it subsequently became clear that it was not a lemma but rather a central problem in the field.”