Geometry and physics have long gone hand in hand. All around us, physical processes play out in geometric terms, such as straight lines (rays of light), ellipses (planetary motion), or parallelograms (the combined effect of two forces). To earlier scientists, this meant that the universe was created to be comprehensible. Kepler went so far as to argue that God, in setting up the natural world, could use pentagons but never heptagons, since the heptagon can’t be constructed with ruler and compass.[1] Kepler’s enthusiasm for geometry still resonates with modern mathematicians, even though we may not share his metaphysical certainties. Our views also differ in another important respect. For Kepler, the elements of geometry, as set out by Euclid, were immutable (after all, they constrained even God). Today it seems clear that, in order for geometric thinking to remain a source of new insights (in mathematics, physics, computer science . . .), geometry must continue to evolve.
One of the current challenges comes from quantum physics, which indicates that space should be an emergent concept, rather than a fundamental one. To a geometer, this is rather disconcerting, like demanding that a painter start without a canvas. As a more easily graspable compromise, we can take our usual Euclidean space as a starting point, and then put that through a process that moves pieces of it around, like a series of small earthquakes (called “quantum corrections”). If the earthquakes get too violent, the process will get out of control, and its outcome must lie beyond geometry. But if the modifications are small enough, we will be able to see a new space gradually emerging as the result. In this article, I will try to explain one such construction. It comes from “mirror symmetry,” which was the topic of the 2016–17 special year in the School of Mathematics. The specific structure governing the process is called the “tropical vertex group,” and it is visualized through “scattering diagrams” (I have no intention of explaining any of those terms; but they do roll off the tongue beautifully). The construction was invented in 2006 by Maxim Kontsevich and Yan Soibelman[2] (Soibelman was a Visitor at the IAS program). Unlike the heptagon, which Kepler was so concerned about, it is still a developing mathematical subject.
When going about the mind-bending business of revisiting our concept of space, how can the imagination keep a foothold? A long-standing tradition is to imagine oneself a traveler in a faraway place. At various times, this kind of fiction has enabled us to conceive of the moon and planets as earthlike bodies;[3] to live in more or less than two dimensions;[4] or to run alongside a beam of light.[5] It will hopefully also help us here.
With that in mind . . . Once upon a time, there were two countries, Northlandia and Southlandia. Due to ideological disagreements, the countries’ maps of the world use slightly different coordinates (x, y). You may bring a South-made map to the North; when crossing the border, you will be handed a small paper slip with the formula for converting one kind of coordinates to the other, so that you can exchange geographical information with the locals. Here’s what the slip says:

When looking at this slip, we see that North and South agree on what the x-coordinate should be (this has to do with the fact that the border between them is a horizontal West-East line), but disagree slightly on the y-coordinate. The strange-looking 0.01 is an arbitrarily chosen small number, measuring the ideological differences (if we replaced it by 0, the discrepancy between coordinate systems would disappear). Such coexisting coordinate systems, called “charts,” are generally unproblematic (just like using degrees Celsius and Fahrenheit doesn’t mean that our notion of temperature is problematic), as long as the conversion rules between them are consistent. To make things interesting, we have to look at a more complicated geography.
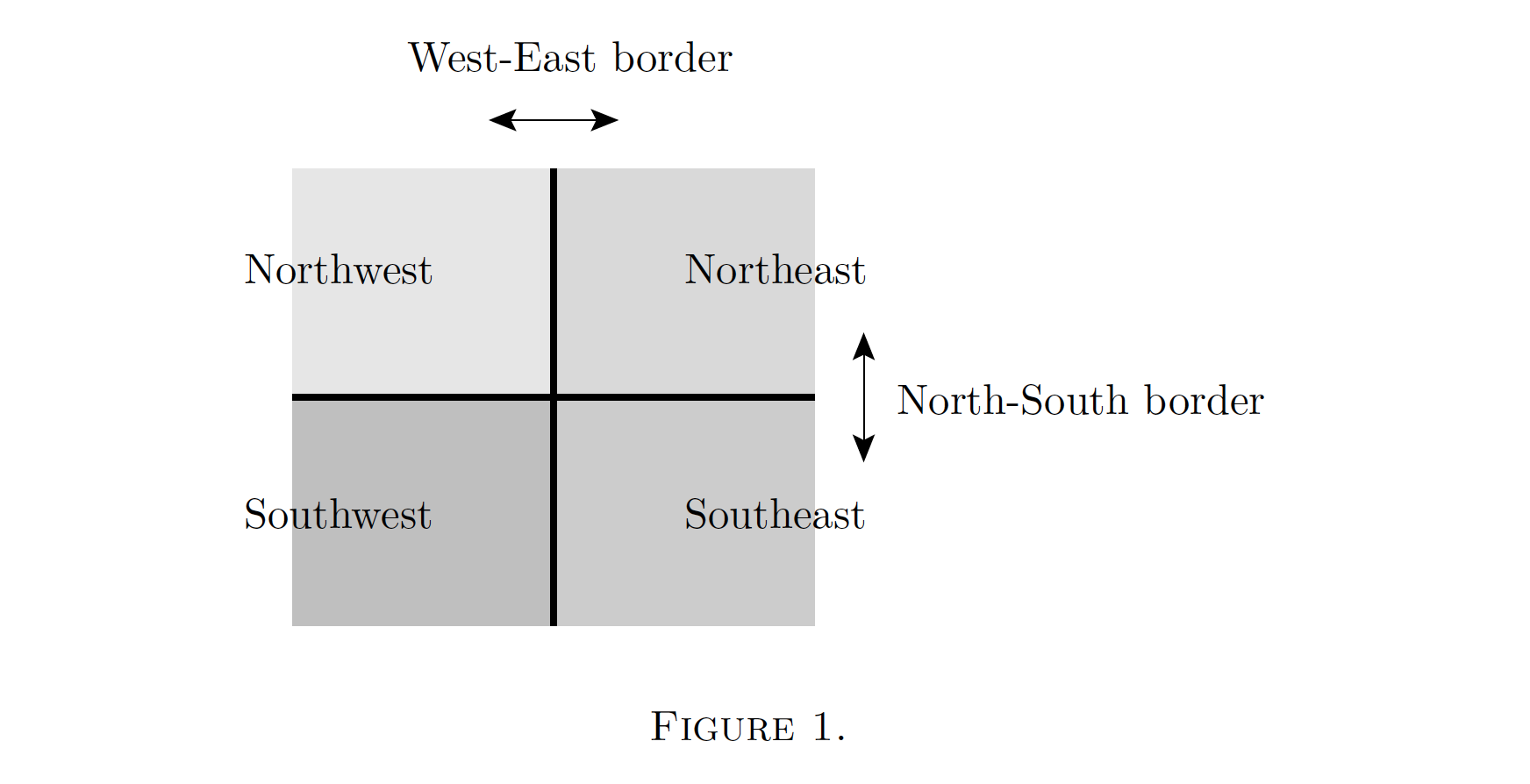
Take four countries, Northwestlandia, Southwestlandia, Southeastlandia, and Northeastlandia (Figure 1). Each has its own coordinate system, and here are the conversion rules handed out at border crossings:

The traveler trying to use these rules will be startled to find that the conversion from, say, Southwestern to Northeastern coordinates depends on whether you go through the Southeast or the Northwest. The difference is very small, on the order of 0.0001, but even the smallest discrepancy leads to logical inconsistencies. After all, the Cathedral of Northeastlandia should always be in the same place, no matter which route you choose on your visit from the Southwest. And if you take a trip all around the continent, the discrepancy means that landmarks in your home country would have shifted slightly when you return. Clearly, our cartography is insufficiently precise.
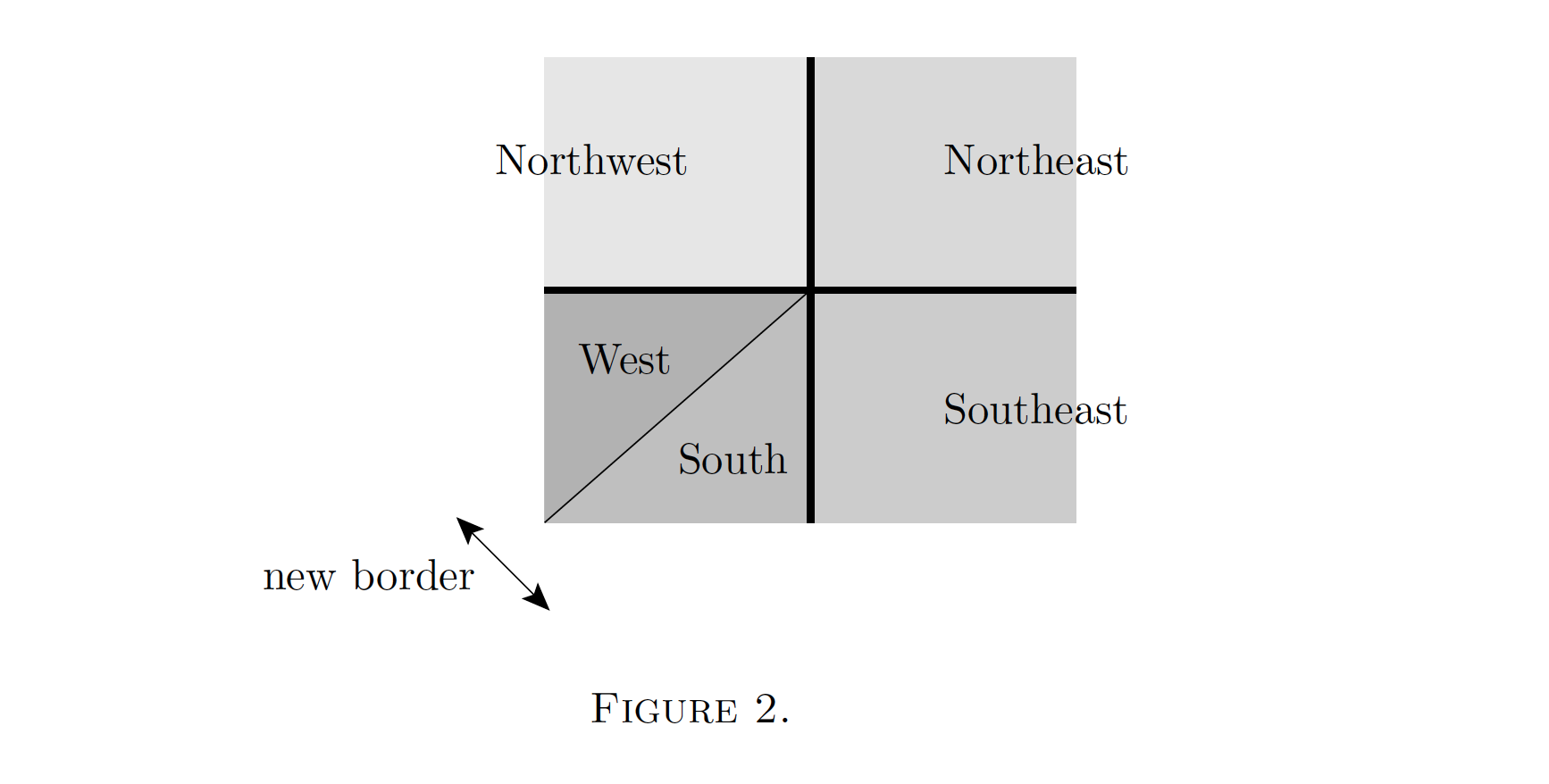
The local cartographers resolved this difficulty in the following way. Southwestlandia should be considered as two provinces, Southlandia and Westlandia, whose maps are not quite the same. When crossing the border from one province to the other (the thinner line in Figure 2), another transition will be necessary, which had not been previously noticed since it’s much less significant than the others:
(x, y) → (x(1 + 0.0001xy), y/(1 + 0.0001xy)).
With that taken into account, consistency is restored, and all landmarks stay in place when travelling, to any order of precision (the mathematical computation which shows that, by following the traveler all around, is simple but still entirely surprising). The appearance of the new border, which gives us five “charts” instead of the original four, is what’s called “scattering” in this context. In (vaguely) physics-inspired terminology, our initial border crossing rules are the initial “first order quantum corrections,” which were given to us as part of the setup of the problem; consistency then forced us to introduce a “second order correction.”
Now let’s go through the same argument, but starting out with slightly different rules:

This is like having each of the previous border crossings repeating twice (say, passport control and then customs), and it gives rise to the same inconsistency. We may think we already know how to address this–let’s repeat the previous trick, splitting one country in two, but now with terms raised to the appropriate power:
(x, y) → (x/(1 + 0.0001xy)4, y(1 + 0.0001xy)4).
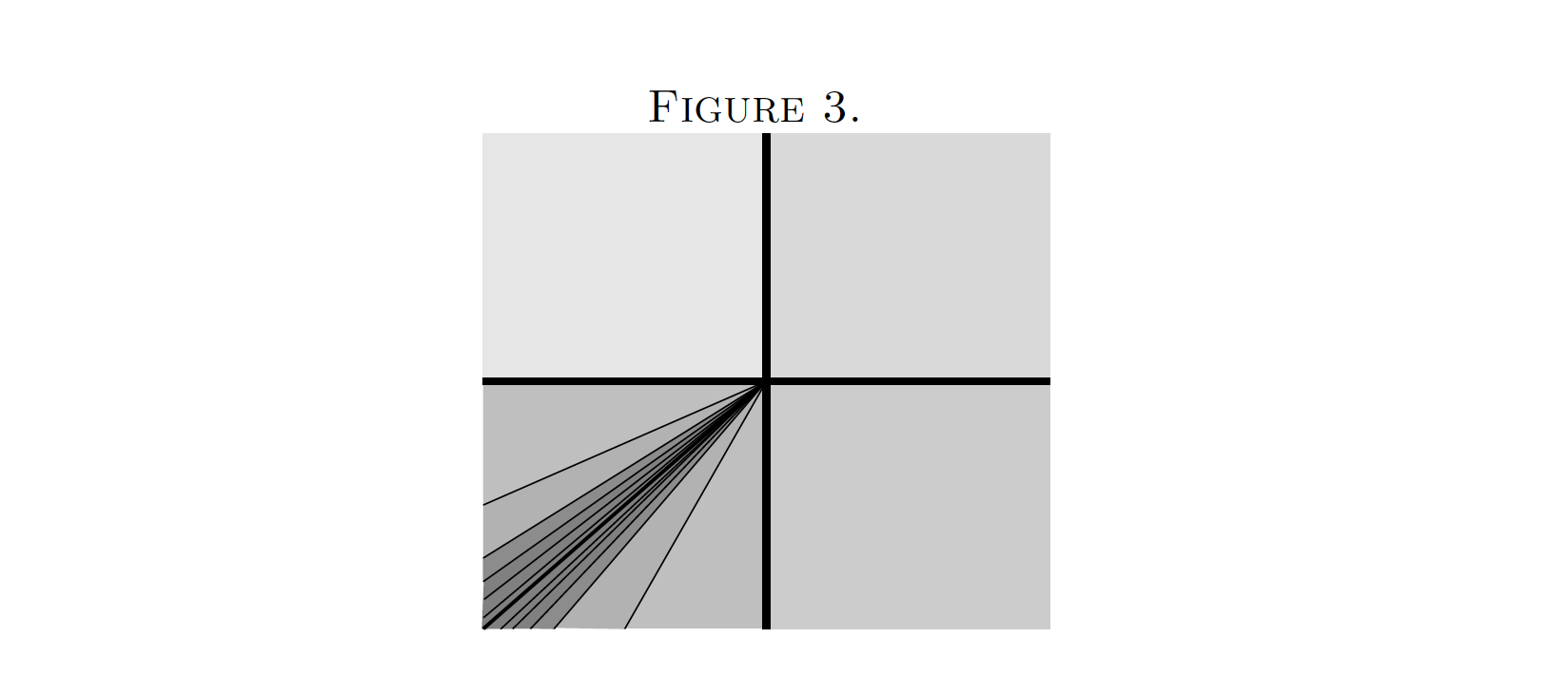
Unfortunately, this does not resolve all the inconsistencies! It leaves errors of order 0.000001. The actual solution involves an infinite number of new borders subdividing the former Southwest territory, which are accompanied by smaller and smaller changes of coordinates (Figure 3). This kind of “infinite factorization” process, involving “quantum corrections” of higher and higher order, is what we’ve been aiming for. As before, the process starts with only the original “first order” North-South and West-East rules. From then on, everything is governed by the need to avoid paradoxes, which will determine the new borders and all the formulae associated with them.[6]
One could argue that what I’ve described is not a complicated geometry, but merely one in which ideological differences (and overly mathematically trained cartographers) have created artificial complications. After all, the countries in the story didn’t undergo any actual earthquakes, only the way in which their maps were related kept changing. This is partly the effect of an unfortunate mix-up of metaphors, and partly a consequence of trying to keep to a specific simple example. One can still agree that describing the relative positions of places in different countries in a consistent way turned out to be unexpectedly difficult, far harder than in the usual Euclidean (x, y) plane; and that is certainly an interesting geometric phenomenon.
Since we’re already casting a critical eye back on our story, how about keeping track of the sizes of the various discrepancies? Undoubtedly 0.0001 is much smaller than 0.01, but small errors can easily accumulate. One would like to say that this not a problem, even for infinitely many border crossings, in the same sense as Achilles overtaking the tortoise wasn’t impossible after all. But are we sure about that? One can circumvent the question by replacing 0.01 with a fictitious infinitely small number; but then, all answers will be in terms of that fictitious number. For the purpose of doing geometry on the resulting spaces, an answer involving just the usual numbers would clearly be more satisfying.[7] The best I can say is that for some problems of this kind, mirror symmetry can be used to show that the infinite process makes sense, by an indirect argument. On the other hand, if you come to tea break at the Institute, it’s quite possible that someone there will be able to suggest a better approach to you!
[1] “[...] quo minus Heptagonus, et caeterae hujus figurae, a Deo fuerint adhibite ad ornatum Mundi.” Harmonices Mundi (1619), Lib. I, Prop. XLV. Kepler’s discussion of such “unknowable” (inscibile) figures is fascinating: he claims that even an Omniscient Mind cannot comprehend them “in a simple action.”
[2] Kontsevich and Soibelman, Affine structures and non-Archimedean analytic spaces, in: The Unity of Mathematics, Birkhauser, 2006.
[3] For an account of how literature and science in the sixteenth and seventeenth centuries worked together on that goal, see: F. Ait-Touati, Contes de la lune: Essai sur la fiction et la science moderne, 2011.
[4] Abbott, Flatland: A Romance of Many Dimensions, 1884.
[5] “Wenn man einer Lichtwelle mit Lichtgeschwindigkeit nachläuft.” Presumably, many readers of this newsletter will know what this refers to. The original reference is: Einstein, Autobiographische Skizze, in: Seelig (ed.), Helle Zeit - Dunkle Zeit. In memoriam Albert Einstein, 1956.
[6] For further developments, see: Gross, Pandharipade, and Siebert, The tropical vertex, Duke Math. J. 153 (2010).
[7] For a related construction where this is clearly an important problem, see: Gaiotto, Moore, and Neitzke, Four-dimensional wall-crossing via three-dimensional field theory, Commun. Math. Phys. 299, 2010.