The Astrophysics Behind LIGO’s Detection

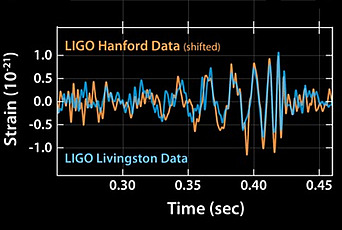
On September 14, 2015, the two detectors of the Laser Interferometer Gravitational-Wave Observatory (LIGO) observed a gravitational-wave signal from the merger of a pair of black holes. While this impressive technological triumph was celebrated around the world, the astrophysical source that emitted the gravitational radiation reminded us to remain humble while making predictions in terra incognita.

Like any antenna, the LIGO detectors were tuned to a particular frequency and to reach some sensitivity. The frequency enables LIGO to detect only mergers involving a pair of massive objects, each of which is much smaller than one thousand kilometers. We only know of two classes of such objects: neutron stars (NSs) and black holes (BHs). The mass of an NS is roughly the mass of our Sun (one solar mass) and its radius is roughly ten kilometers (somewhat larger than Mount Everest). It is so dense that the velocity required to escape from its surface is not much smaller than the speed of light. The masses of BHs, on the other hand, vary significantly; while some of them have masses of millions or billions of solar masses with radii much larger than relevant for LIGO, some of them are smaller, with masses of roughly ten solar masses and radii of tens of kilometers, which satisfy LIGO’s frequency requirements. The velocity required to escape from a BH surface is exactly the speed of light, as the name suggests.

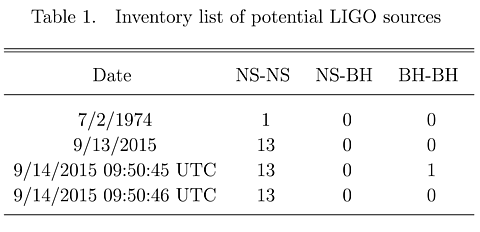
To estimate the required sensitivity of the detectors, we must know how many pairs of each type (NS+NS, NS+BH, or BH+BH) exist in the universe and how long it would take for them to merge. This provides the rate of such mergers throughout the universe. The rarer such systems are, the larger the volume the detectors have to monitor, which in turn determines their sensitivity. The inventory of such systems that are known is summarized in Table 1. During the construction of the LIGO detectors, only one type of system was known: NS+NS. The few known examples of this system were sufficient for Sterl Phinney to estimate, in 1991, the required sensitivity of the detectors. LIGO’s goal is to detect an NS+NS merger at a distance of 650 million light years (compared to the edge of the observable universe of about 46.5 billion light years away) or equivalently to monitor about one million galaxies to observe a few NS+NS merger events every year. There were no known examples of other types of systems (NS+BH and BH+BH), which would produce stronger gravitational waves as they merge, making any useful predictions by astrophysicists impossible. The ambitious effort to reach the required sensitivity to detect NS+NS mergers was done in stages, with each improvement in sensitivity being tested for a period of time. Long before they reached the required sensitivity to detect an NS+NS merger, the LIGO detectors observed a BH+BH merger at a distance of about one billion light years away. It was impossible to robustly predict this merger that happened one billion years ago, as it was the first time in human history that any evidence for such a system was obtained. Unfortunately, this system no longer exists, as it merged into a single larger BH.

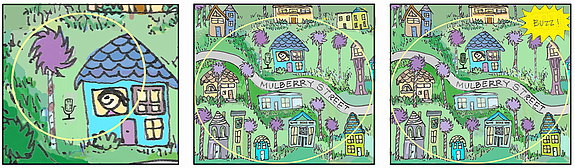
Let me try to explain the previous paragraph with a simple analogy. Kay McLigo is a curious girl living on Mulberry Street. In her backyard, there is a Neutrula tree. According to a tale that her mother tells her, a Neutrula tree produces a fruit exactly every one hundred years. Nobody has ever seen this fruit, since a Bar-ba-loot bear eats it the moment it pops. However, the popping of the fruit makes a very low hum (this is how the Bar-ba-loot bears find it), and you may hear it if you listen very carefully. Kay McLigo is a smart girl, so she does not believe everything her mother tells her, and instead she decides to confirm this tale with a simple experiment. She places a microphone in her backyard, and she looks for the hum in her recordings. Unfortunately, the microphone can only record hums in Kay McLigo’s own backyard, so she realizes that she would have to wait roughly one hundred years. Since Kay McLigo wants to know the answer much sooner than that, she decides to replace the small microphone with a larger, more sensitive microphone. The larger microphone can also record hums from other Neutrula trees on Mulberry Street, and Kay McLigo estimates that there are about ten such trees, meaning she only has to wait for roughly ten years. Kay McLigo is quite happy with her new instrument (she has no plans of moving out of her parents’ house for the next ten years or so). However, after only six months, her microphone records a buzz (not a hum)! Very excited, Kay McLigo tells this to her mother, who has a vague memory of her own mother telling her about invisible trees, known as Blackhula trees. Blackhula trees are similar to Neutrula trees, but the popping of their fruit makes a very low buzz. Eureka! Kay McLigo has made a wonderful discovery, which also allows her to estimate how many invisible Blackhula trees grow on Mulberry Street.

Returning to LIGO’s discovery, some light can be shed on the origin of this BH+BH system. The detected signal allows us to estimate the mass of each BH, as well as the average spin (or rotation) of the BHs. One likely scenario for the origin of this system is two massive stars orbiting each other. Each of these massive stars explodes as a supernova, leaving a BH remnant behind. Before the second star explodes, the system consists of a BH and a massive star. The longer it takes them to orbit each other, the further they are from each other. If we assume that as the massive star explodes the separation between the old and new BHs is roughly the same as the separation between the massive star and the BH, then we can directly calculate how long it would take for the BH+BH system to merge. If they are too far apart, they will not merge within the age of the universe (roughly fourteen billion years). The result of this calculation is that the massive star and the BH complete a full revolution around each other faster than about once per day. The closer they are, the faster it takes the BH+BH system to merge. In a paper¹ that I coauthored with Professor Matias Zaldarriaga, Junior Visiting Professor Juna A. Kollmeier of Carnegie Observatories, and Roni Waldman of Hebrew University, it was shown that the merger time of the BH+BH system must be longer than about 100 million years by exploiting the low observed average spin of the BHs. If the merger time was shorter than this constraint, then the BH and the massive star would have been very close to each other, and in this case, the gravity of the BH would have spun up the massive star using tides, leading to a tidal locking of the massive star. This is similar to the tidal locking between Earth and its moon, in which the spin of the moon is exactly equal to its rotation around Earth (meaning that it takes the moon one month to complete a full revolution around its axis; this is also the reason why only one side of the moon is visible from Earth). The tidal locking of the massive star would make its spin very high, and this would later lead to a high spin of the remnant BH that would contradict the low observed average spin of the BHs. On December 26, 2015, LIGO observed another BH+BH merger, and many more BH+BH systems will be discovered in the upcoming years. With them, much stronger constraints will be placed on the origin of these spectacular systems.

What about the NS+NS systems? Kay McLigo is still looking for a Neutrula tree’s hum in her recordings . . .

¹ Doron Kushnir, Matias Zaldarriaga, Juna A. Kollmeier, and Roni Waldman, “GW150914: Spin-based Constraints on the Merger Time of the Progenitor System” (2015): http://arxiv.org/pdf/1605.03839v2.pdf.