Volumes of Hyperbolic Link Complements

During the 2015-16 academic year, the School of Mathematics hosted a program on the topic of geometric structures in three dimensions. This article is an adaptation of a talk I gave in fall 2015, as part of the School's biweekly "Mathematical Conversations" series, designed for a general mathematics audience. Below, I introduce a particular three-dimensional geometric structure, which is ubiquitous in the study of knots and links, and focus on topology in three dimensions, its relation to geometry, and the following questions: What is three-dimensional topology? What is hyperbolic geometry? What are the volumes of link complements?

What is three-dimensional topology?

Topology has its origins in the work of Henri Poincaré, who wanted to study the global structure of solutions to differential equations. Poincaré coined his theory analysis situs, but eventually it became known as the modern theory of topology.

Topology codifies the notion of continuity, meaning the identification of global properties of spaces that do not change under small (local) deformations without cutting or gluing. Two spaces are equivalent if one can be deformed to the other.

Topologists are fond of saying that they cannot distinguish a doughnut from a coffee mug. They call such objects homeomorphic, which may be demonstrated by deforming one to the other as if they were made of clay.

However, what about this coffee mug?

These objects are still intrinsically equivalent (homeomorphic), but cannot be deformed one to the other in three-dimensional space. We need a doughnut to sit differently in three-dimensional space.

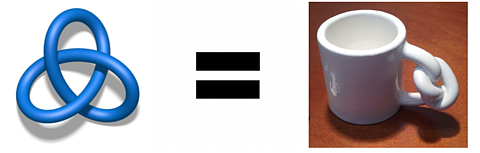
Topologists call these doughnuts knots, referring to closed loops of string.

How do we tell when two doughnuts (or knots) are not equivalent to each other by deformation (isotopy)?

A knot complement is what is left when you remove a knot from space. For example, take an inner tube (surface of a doughnut), puncture it with a little hole, and turn it inside out.

What happens if we do this to an inner tube tied in a figure 8? We get a figure-8 knot complement.

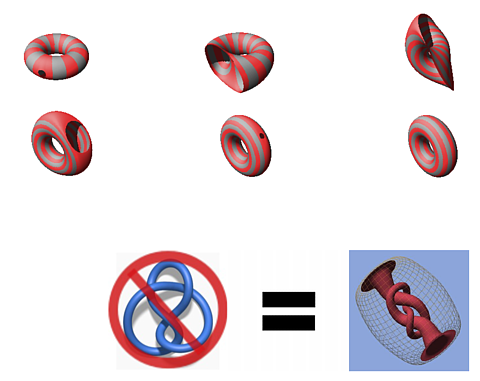
If we can distinguish knot complements (up to homeomorphism), then we can distinguish the knots up to deformation (isotopy). Under a deformation of a knot, the knot complement gets carried along like an aether. The goal of knot theory is to find invariants to distinguish knots up to deformation, so that two knots with different invariants could not possibly be isotopic. I’ll discuss one such invariant, which is based on the knot complement.

Cameron Gordon and John Luecke proved in 1989 that two knots with homeomorphic complements are equivalent up to isotopy and taking a mirror image.

It is a bit hard to visualize, but it could a priori be possible that a homeomorphism between two knot complements might not extend over the 3-sphere. There exist such knots in other 3-manifolds, and there exist many links with homeomorphic complements.

What is hyperbolic geometry?

Non-Euclidean (or hyperbolic) geometry was discovered by János Bolyai (1832) and Nikolai Lobachevsky (1830). The shortest distance between two points is a line, but the parallel postulate fails: lines have many parallels (that do not meet). In two dimensions, hyperbolic geometry may be modeled by straight lines in a disk (the Klein model), arcs of circles perpendicular to the boundary of a disk (the Poincaré model), or semicircles perpendicular to the x-axis in the upper half plane.

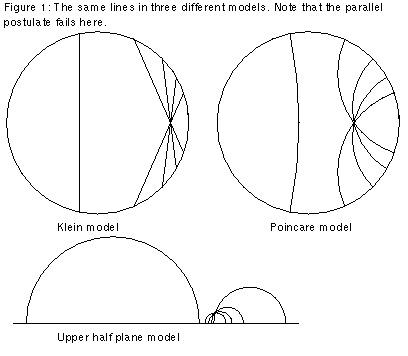
A tactile demonstration of the hyperbolic plane may be crotcheted.

To visualize what is meant by 3-dimensional hyperbolic geometry, a rich area of interest for mathematicians and physicists, consider a chunk of glass sitting on a table, such that the speed of light n is proportional to the height above the table. Light will follow a minimal path in the glass, which is a semicircle or line perpendicular to the table surface.

This gives a physical approximation of the upper-half space model of hyperbolic space. Hyperbolic distance is measured in the minimal time it takes for light to get from point a to point b. Light will follow geodesics (the paths of shortest distance).

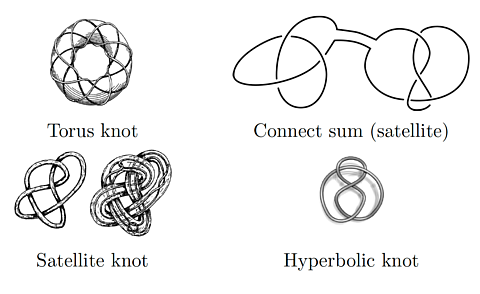
A fundamental discovery of Bill Thurston in the 1970s is that “most” knot complements admit a geometry modeled on hyperbolic geometry. There is a trichotomy: a knot is either a torus knot (sitting on the surface of a standard doughnut), a satellite knot (made by tying a knot within a knot), or else is hyperbolic.

Hyperbolic Volume

A region in the upper-half space has a hyperbolic volume, obtained by integrating 1/n³ over the region.

The hyperbolic volume of this knot complement = 2.0289.

Thurston's theorem is much more general and applies to links (collections of disjoint knots) as well. Here are some examples of links with hyperbolic complements:

A theorem by George Mostow implies that a hyperbolic link admits a unique hyperbolic structure of finite volume. Thus, the hyperbolic structure becomes an invariant of the link complement.

What would it look like to be inside of a space with hyperbolic geometry?

Here is a rendition of the universal cover of the Borromean rings:

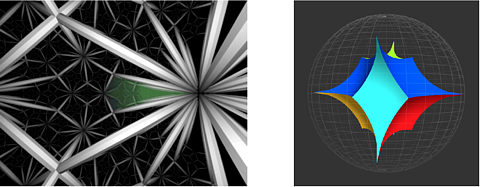
This hyperbolic structure has finite volume, the volume of a fundamental domain (see the video Not Knot, among the references below, for a visualization of the polyhedron on the right).

The volume is:

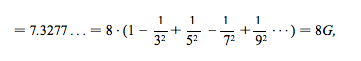
where G is known as Catalan's constant. It is unknown if this constant is irrational!

The volume is a very powerful invariant of link complements. Thurston and Troels Jørgensen showed that for any given volume, there exists only a finite number of link complements with that volume.

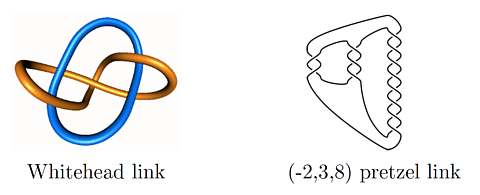
For example, these two links both have volume 4G = 3.66.

Caveat: There may be many hyperbolic links with homeomorphic complements, and thus the same volume, although it is understood how they can differ.

Even though these two link complements have the same volume, they are not homeomorphic.

There are certain geometrical invariants in the upper-half space model that distinguish them (computed with the program SnapPy by Marc Culler and Nathan Dunfield, based on the program SnapPea by Jeff Weeks). The links in the previous figure have the same volume, but are distinguished by their horoball diagrams (computed by SnapPea):

Images: Whitehead link horoball diagram (left); (-2,3,8) pretzel link horoball diagram (right)

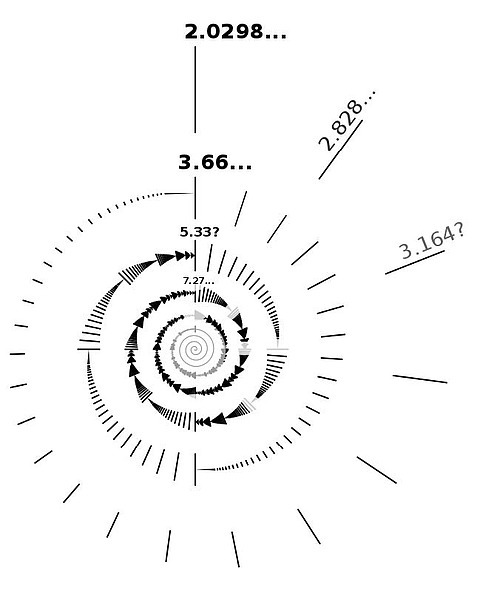
Moreover, volumes are “well-ordered": any decreasing sequence of distinct hyperbolic link volumes is finite (i.e., limits of volumes can only increase). Thus, they are sometimes referred to as the “volume spectrum," by analogy. For example, consider these twist knots:

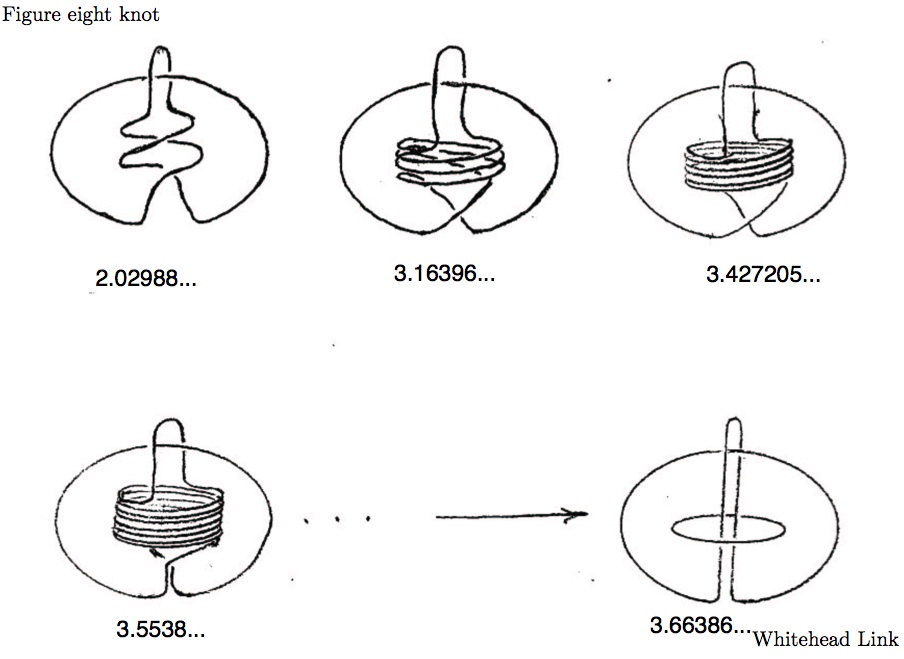
Their volumes limit to that of the Whitehead link complement.

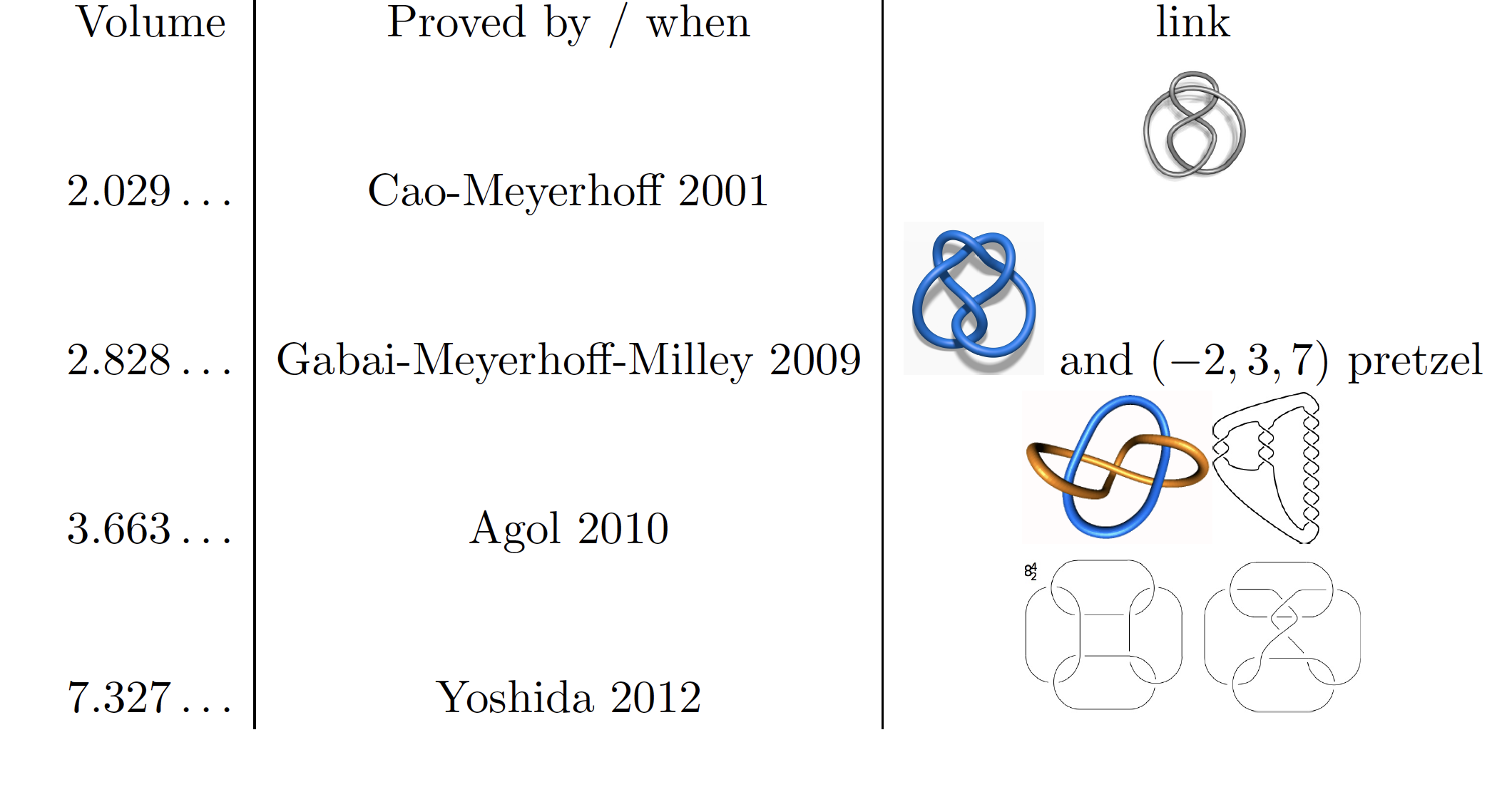
The smallest link volumes of 1, 2, and 4 components and the second smallest knot volume have been proved to be:

Open Questions

The proofs of the first two theorems are computer aided. The proofs of the last two theorems make use of a theorem of A.-Storm-Thurston from 2007, which in turn uses such technology as minimal surfaces and Ricci flow used by Grigori Perelman to solve Thurston’s geometrization conjecture and the Poincaré conjecture.

Open question: What is the smallest hyperbolic link complement with three components? Conjecturally it is the 3-chain link with volume = 5.33348.

What is the smallest volume hyperbolic link complement with n components?

In his thesis, Rupert Venzke pointed out that the smallest volume links up to ten components seem to be minimally untwisted chain links. For eleven or more components, he pointed out that these are beaten by cyclic covers of the Whitehead link complement (this was proven by Kaiser-Purcell-Rollins in 2012 for n ≥ 60, and holds numerically in general).

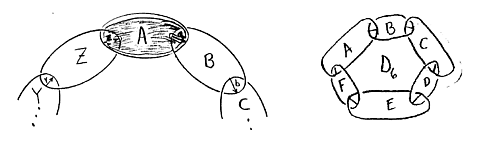
Conjecture: The minimal volume of an n-component link ÷ n → 4G.