Links, Molecules, and Quantum States

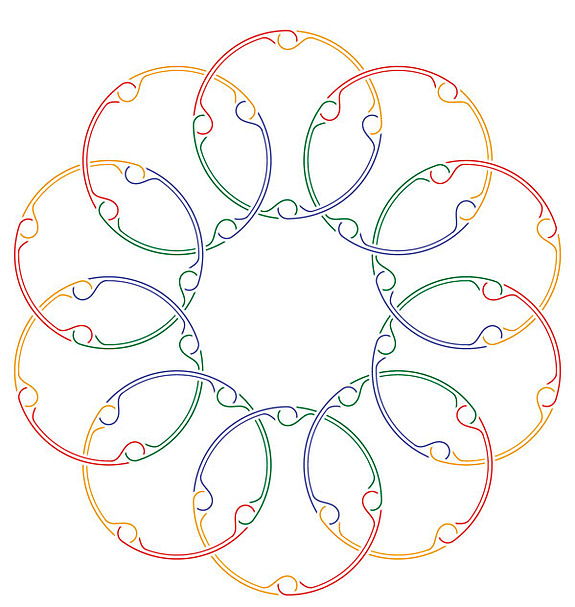
For a long time time, I have had a profound interest in studying “higher order structures” of various kinds. What is a higher order object? I will not here attempt to give a definition, but rather illustrate by examples what I have in mind.

In topology, we study knots and links. A link is given by a collection of circles or rings embedded in three-dimensional space. If the link has just one ring, we call it a knot. There is a plethora of links, hence I have picked out special families in order to illustrate certain types of higher order structures. Let us first look at three well-known links:

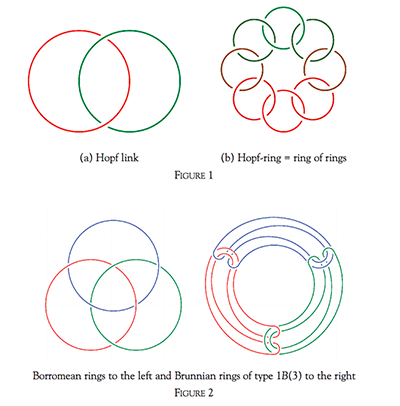
Definition. (i) A link consisting of n rings has the Brunnian property if and only if any sublink of (n –1) rings is unlinked.
(ii) A link consisting of n rings has the Borromean property if and only if any two rings are unlinked.
For n=3, the two properties coincide as we see in Figure 2.

How do we describe such linkings? Staying on the rings, the topology is simple, but in the complement, it is complicated. Hence, we study the topology of the complement K=R³ – Link.
Hopf links are detected by cohomological cup products and Borromean rings by Massey products. In addition, other invariants like the Jones polynomials pick up linkings of this kind. What about higher order links?

In Figure 3, we consider rings of rings based on the Hopf link:

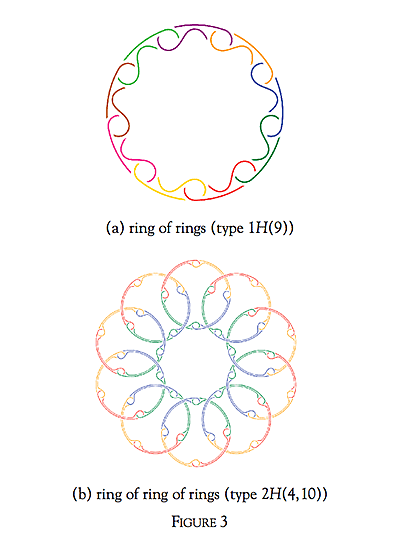
We call these Hopf rings of first and second order. This linking is detected by an extended version of Massey products.

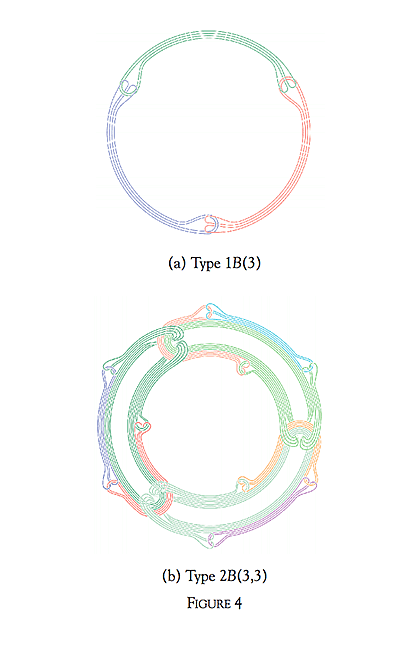
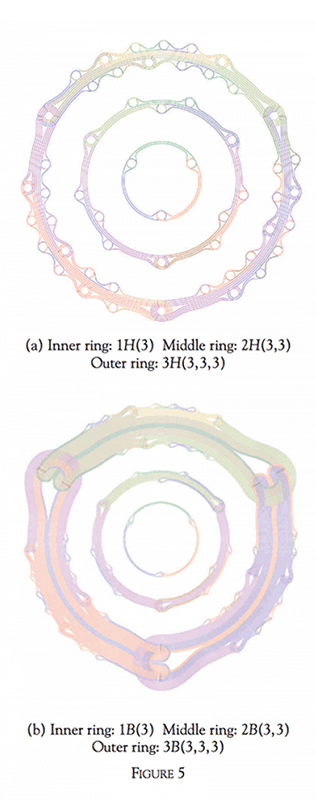
Let us now build a family of Brunnian rings starting with a Brunnian ring as in Figure 4(a). We take three of these, bend them, and hook them up in a Brunnian way to a Brunnian ring of Brunnian rings—a second order Brunnian ring as in Figure 4(b).

This process can be iterated by taking second order rings and forming third order rings, etc. The number of rings at each level can vary. Hence we get a family of Brunnian rings n-B(k1,k2,…,kn) which captures the idea of being of higher order. This family is a good guide for our intuition. In Figure 5, we show the lower stages of the Hopf-family and the Brunnian family. Good invariants are needed to describe efficiently this kind of higher order linking.

In synthetic chemistry, it has been a challenge to synthesize various knots and links. The first one to synthesize Borromean rings was Ned Seeman at New York University using DNA molecules. We have teamed up, and he is now working on the synthesis of higher order links—in particular, second order Brunnian rings. It will be interesting to see whether new material properties will appear.

In 1970, the Russian physicist V. Efimov predicted new counterintuitive quantum states where three particles are bound, but not two by two. This is quite analogous to the Borromean and Brunnian property. Experimentally, such states were not observed until 2006 in ultracold caesium gases.

This raises the following interesting question: Does there exist a family of quantum states analogous to the Brunnian family?

We know that this is the case at the bottom level, but what about higher up. Trimers exist, what about trimers of trimers? The question is wide open! Independent of the role of these higher order links in mathematics, chemistry, and physics, they have an intrinsic beauty that everybody can enjoy.

Borromean rings have a long history. They appeared in old pieces of art in Afghanistan, in the form of triangles in Nordic mythology, and in the coat of arms of the Italian Borromeo family. In the Christian church, they have been used as a symbol of the Holy Trinity. ■