The Odd Couple: Quasars and Black Holes

Black holes are among the strangest predictions of Einstein’s general theory of relativity: regions of spacetime in which gravity is so strong that nothing—not even light—can escape. More precisely, a black hole is a singularity in spacetime surrounded by an event horizon, a surface that acts as a perfect one-way membrane: matter and radiation can enter the event horizon, but, once inside, can never escape. Remarkably, an isolated, uncharged black hole is completely characterized by only two parameters: its mass, and its spin or angular momentum.
Laboratory study of a macroscopic black hole is impossible with current or foreseeable technology, so the only way to test these predictions of Einstein’s theory is to find black holes in the heavens. Not surprisingly, isolated black holes are difficult to see. Not only are they black, they are also very small: a black hole with the mass of the Sun is only a few kilometers in diameter (this statement is deliberately vague: because black holes bend space, notions of “distance” close to a black hole are not unique). However, the prospects for detecting black holes in gas-rich environments are much better. The gas close to the black hole normally takes the form of a rotating disk, called an accretion disk: rather than falling directly into the black hole, the orbiting gas gradually spirals in toward the event horizon as its orbital energy is transformed into heat, which warms the gas until it glows. By the time the inward-spiraling gas disappears behind the event horizon a vast amount of radiation has been emitted from every kilogram of accreted gas.
In this process, the black hole can be thought of as a furnace: when provided with fuel (the gas) it produces energy (the outgoing radiation). Einstein’s iconic formula E=Mc2 relates mass M and the speed of light c to an energy E called the rest-mass energy. Using this relation, there is a natural dimensionless measure of the efficiency of this or any other furnace: the ratio of the energy it produces to the rest-mass energy of the fuel that it consumes. For furnaces that burn fossil fuels the efficiency is extraordinarily small, about 5 x 10-10. For nuclear reactors using uranium fuel, the efficiency is much better, around 0.1 percent; and for the fusion reactions that power the Sun and stars, the efficiency can reach 0.3 percent.
Black-hole furnaces can have even higher efficiency than any of these: between 10 and 40 percent. In the unlikely event that we could domesticate black holes, the entire electrical energy consumption in the United States could be provided by a black-hole furnace consuming only a few kilograms of fuel per year (an additional benefit of black holes is that they can consume radioactive waste, rather than generating it!).
Despite the relatively low efficiency of fusion reactions, most of the light in the universe comes from stars. Most of these stars are organized in galaxies. Our own galaxy contains a few tens of billions of stars arranged in a disk; the nearest of these is about 1 parsec (3.26 light years) from us, and the distance to the center of our galaxy is about 8 kiloparsecs (about 26,000 light years). The diffuse light from distant stars in the galactic disk is what we observe as the Milky Way.
A small fraction of galaxies contain mysterious compact light sources near their centers, called active galactic nuclei. The brightest of these are the quasars; remarkably, quasars can emit up to 1013 times more light than the Sun, thereby outshining the entire galaxy that hosts them. Even though quasars are much more rare than galaxies, they are so bright that they contribute almost 10 percent of the light emitted in the universe.
Ironically, the extraordinary luminosity of quasars is what made them hard to discover. Except in a few cases, they are so bright that the host galaxy cannot be seen in the glare from the quasar, and so small that they look like stars (in fact, “quasar” is a contraction of “quasi-stellar object”). Thus, even the brightest quasars are usually indistinguishable from millions of stars of similar brightness. Fortunately, some quasars are also strong sources of radio emission, and in 1963 this clue enabled astronomers to identify a radio source called 3C 273 with a faint optical source that looked like an undistinguished star. With this identification in hand, Maarten Schmidt at Caltech was able to show that 3C 273’s spectral lines were redshifted—Doppler shifted by the cosmological expansion of the universe—to wavelengths 16 percent longer than laboratory spectra, and thus that 3C 273 was at a distance of eight hundred megaparsecs, ten million times further away than it would have been if it were a normal star.
By now we have discovered almost one hundred thousand quasars. Most were formed when the universe was 20–30 percent of its current age, and by now the population has declined from its peak by almost two orders of magnitude, presumably because the fuel supply for quasars is drying up as the universe expands at an accelerating rate.
How can quasars emit so much energy? The suggestion that they are black-hole furnaces was made soon after they were first discovered. But in the 1960s the black hole was a novel and exotic concept, and staggeringly massive black holes (roughly one hundred million solar masses) were required to explain quasar properties. Thus, most astronomers quite properly focused on more conservative models, such as supermassive stars, dense clusters of ordinary stars or neutron stars, and collapsing gas clouds. Over the next two decades, however, all of these models proved unable to explain the growing body of observations of quasars. Furthermore, other studies showed that the formation of massive black holes in the centers of galaxies is natural and perhaps even inevitable.
A number of indirect but compelling arguments also support the black-hole furnace hypothesis. For example, the luminous output of a bright quasar over its lifetime corresponds to a rest-mass energy of about one hundred million times the mass of the Sun. If this were produced by the fusion reactions that power stars with the efficiency of 0.3 percent given earlier, the required mass of fuel would be almost the total of all the stars in our galaxy. There is no plausible way to funnel this much mass into the tiny region close to the black hole. On the other hand, for a black-hole furnace the efficiency is 10 percent or more, so the required mass is less than 109 solar masses, and this much gas is not hard to find close to the center of many galaxies. Thus, the black-hole furnace is the only model that does not exhaust the host galaxy’s fuel budget.
A second argument concerns the size of quasars. Quasars vary irregularly in brightness on timescales as short as weeks. It proves quite difficult to construct any plausible model of a luminous astrophysical object that varies strongly on a timescale smaller than the light-travel time across the object: different parts of the object are not causally connected on this timescale, so they vary independently and their contributions tend to average out. Thus the size of the most rapidly varying quasars must be less than the distance light travels in a few weeks, around a few hundredths of a parsec or a few thousand times the Earth-Sun distance. Such distances are large by our standards but extremely small on galactic scales, a millionth of the size of the galaxy as a whole. A black hole of one hundred million solar masses and its surrounding accretion disk would fit comfortably inside this volume—its event horizon has a radius of about the Earth-Sun distance—but almost all of the alternative models for quasars fail to do so.
A third argument emerges because some quasars emit powerful jets of plasma that extend for up to a megaparsec (see Figure 1), probably collimated and accelerated by magnetic fields near the black hole. The production of these jets is not so remarkable: for example, various kinds of star also produce jets on a much smaller scale. However, quasar jets typically travel at close to the speed of light, and there is no plausible way to produce such high velocities except close to the event horizon of a black hole. Moreover, the jets are accurately straight, even though the innermost parts of the jet were emitted a million years after the material at the far end. Thus, whatever structure collimated the jet must maintain its alignment over several million years; this is easy if the jets are squirted out along the axis of a spinning black hole, but difficult or impossible in other quasar models.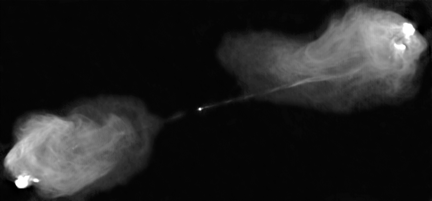
Based on these and other arguments, there is near-complete agreement that the power source for quasars is accretion of gas onto black holes of a hundred million solar masses or more. Accepting this model leads to a simple syllogism: if the number of quasars shining now is far smaller than when the universe was young, and quasars are black-hole furnaces, then many “normal” galaxies should still contain the black holes that used to power quasars at their centers, but are now dark. Can we find these “dead quasars” in nearby galaxies?
An important guidepost in this search came from the Polish astronomer Andrzej Sołtan. The universe is homogeneous, so on average the energy density in quasar light must be the same everywhere in the universe (here average means averaged over scales greater than about ten megaparsecs, which is still small compared to the overall “size” of the universe, a few thousand megaparsecs). We can measure this energy density by adding up the contributions from all the quasars found in surveys. If this energy were produced by black-hole furnaces with an efficiency of 10 percent, for example, then a mass M of material accreted by black holes would produce 0.1Mc2 in quasar light. Similarly, if the average mass density of dead quasars is ρ, then the energy density of quasar light must be 0.1ρc2.
Since we know the latter figure, we can invert the calculation to determine the mass density of dead quasars. The power of this argument is that it requires no assumptions about the masses or numbers of black holes; no knowledge of when, where, or how quasars formed; and no understanding of the physics of the quasar furnace except its efficiency. Sołtan’s argument tells us that the mass density of dead quasars should be a few hundred thousand solar masses per cubic megaparsec, compared to a density of large galaxies of about one per hundred cubic megaparsecs. What it does not tell us is how common or how massive individual dead quasars are: on average there could be, for example, one dead quasar of ten million solar masses in every galaxy, or one of one billion solar masses in 1 percent of galaxies.
Stars that come under the influence of the black hole’s gravitational field—typically those within a distance of a parsec or so—are accelerated to higher velocities. This acceleration leads to increased Doppler shifts, which broaden the spectral lines from the collective stellar population. The search for this effect in the centers of nearby galaxies began around 1980 and yielded evidence for black holes—or, at least, for massive dark objects—in a handful of cases. These results were tantalizing, but incomplete: the problem was that the angular resolution of ground-based telescopes is limited by blurring caused by the atmosphere, so the effects of a black hole could be detected only in the closest galaxies. This problem was one of the motivations for constructing the Hubble Space Telescope, which at the time of its launch in 1990 had roughly ten times the angular resolution of the best ground-based telescopes. Since then the Hubble Telescope has devoted thousands of hours to the hunt for black holes at the centers of galaxies, and this search has confirmed the early ground-based detections in nearby galaxies and produced firm evidence for massive dark objects in several dozen more distant ones. We believe that the massive dark objects observed by Hubble are black holes because the alternatives (for example, a dense cluster of low-luminosity stars) are far less plausible. In recent years the search for dead quasars has been resumed by ground-based telescopes, now using adaptive optics that corrects for atmospheric blurring in real time, providing angular resolutions that equal or exceed Hubble’s.
Our own galaxy also contains a black hole. Very close to the center of the Milky Way is a compact source of strong radio emission known as Sagittarius A*. High-resolution infrared observations reveal a handful of bright stars within a few hundredths of a parsec from Sagittarius A*. The positions and velocities of these stars have been tracked, some for as long as two decades; in particular, the star S2 has an orbital period of only 15.8 years and now has been tracked through more than one complete orbit (Figure 2). Using first-year mechanics, we can deduce from this orbit that the star is orbiting a body that is located at Sagittarius A*, that this body has a mass of 4.3 million solar masses, and that the size of this body is less than only one hundred times the Earth-Sun distance. This extreme concentration of mass is incompatible with any known long-lived astrophysical system other than a black hole.
What have we learned more broadly about the relation between black holes and galaxies? First, black holes seem to be present in most galaxies. Second, in most cases the black-hole mass is about 0.2 percent of the mass of the stars in the galaxy. But are the black holes that we are finding really dead quasars? From galaxy surveys we can determine the average mass density in stars in the local universe, and since black-hole masses are typically 0.2 percent of the stellar mass in a galaxy, we can estimate the average mass density of black holes. Sołtan’s argument, described earlier, gives the average mass density of dead quasars from completely different data. The two estimates agree to within a factor of about two—well within the uncertainties—so there is little doubt that the black holes we have found are indeed the ash from quasars. Thus quasars—one of the most remarkable components of the extragalactic universe—turn out to be black holes—one of the most exotic predictions of twentieth-century theoretical physics.
One of the most profound unanswered questions about these objects is the relation between black holes and galaxy formation. Although black holes make up only a fraction of a percent of the mass of the stars in galaxies, the energy released in forming them is hundreds of times larger than the energy released in forming the rest of the galaxy. If even a small fraction of this energy were fed back to the surrounding gas and stars, it would have a dramatic influence on the galaxy formation process, perhaps blowing the gas out of the galaxy and thereby quenching the formation of new stars. Are black holes and quasars an interesting by-product of galaxy formation that has no influence on the formation process, or do they play a central role in regulating it? More succinctly, do galaxies determine the properties of quasars or vice versa?
A second profound question is whether these black holes can serve as physics laboratories. All of the tests of Einstein’s theory so far—which it has passed with flying colors—have been conducted in weak gravitational fields, such as those on Earth or in the solar system. Thus we have no direct evidence that the theory works in strong gravitational fields. Many naturally occurring processes near black holes in galaxy centers, such as swallowing of stars and black-hole mergers, may potentially be measured with the next generation of astronomical observatories. Can we understand these processes well enough to test the predictions of general relativity in strong gravitational fields, and will Einstein turn out to be right?


