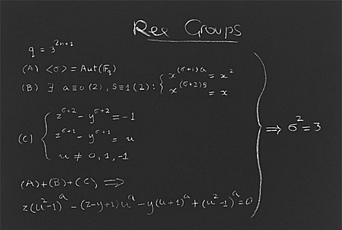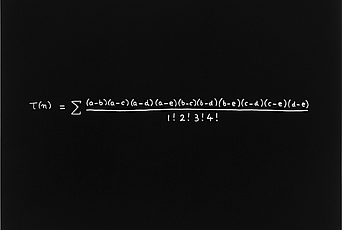My earliest mathematical memories involve my father. One is of a walk from home to the edge of downtown Metuchen (the tiny central Jersey town where I grew up), to a little luncheonette called The Corner Confectionary. This wasn’t a frequent or regular event, but from time to time on a weekend morning we’d make our way there. It was about a mile as we first walked to the corner of Rose Street and Spring Street and then strolled up Spring—a beautiful leafy street with huge oak trees on which our friends the Kahns lived—to finally reach Main Street where we made a quick left, crossed the bridge over the railroad tracks to arrive at the store. I can still see its layout, even in the cluttered neural attic that holds my childhood memories: cash register by the door, rack filled with newspapers, magazines, and comic books, ice cream treats in the back corner, and of course, the long counter, lined with stools on which we would sit and spin—until told to stop.
The walk I remember—or to be completely honest, seem to remember—involved fractions, or rather dividing up pieces of pie. That’s how my Dad framed it. We were puzzling over how to divide fairly a pie among friends. I could see it was easy to make two or four even pieces of pie or eight, but three or five or six would have some challenges. We took our time getting to The Corner Confectionary, and we also took our time thinking about and talking about the basic properties of numbers and division; it was a leisurely walk through the neighborhood, accompanied by a leisurely walk through ideas, that soon led me to the exciting idea that twelve was a great number. Twelve could be divided by two, three, four, and six—that’s a lot of numbers! If I had a pie in twelve pieces, it would be pretty easy to accommodate lots of different groups of friends for dessert. It seemed to me that twelve was a much better number to base things on than the number ten, which could only be divided into two things or five things. I do recall being very happy with the discovery that some numbers held more possibilities than others, a notion of possibility as expressed through division and multiplication and pie. I also recall how happy I was to have shared this little discovery with my father, the physicist, on a bright fall morning in my little town as we walked to get a morning treat.
My other early memory of mathematics is not one memory, but a whole collection of memories, accumulated over many visits to my father’s office in the physics department at Rutgers University where he taught. A visit to that office was a treat, especially for access to the blackboard, always full of equations when I arrived, incomprehensible, but to me, beautiful, elegant, and full of mystery. The pads of paper and notebooks on his desk were full of similar beautiful mysteries. Nothing was more fun than trying to replicate these hieroglyphics on my own—the big looping integral signs (as I would discover later) or the snakey squiggles of a xi, psi, or any Greek letter. I didn’t know what any of it meant, and the truth is, I didn’t really care—I just liked the way it looked and the fact that these symbols meant something to someone, made me feel like I was writing away in a beautiful calligraphic code. I was proud that my father could make such beautiful looking things and they were meaningful to him and to others. I thought that one day, I might like to do that myself.
These are my stories about beauty in mathematics. I think they share much with the stories accompanying the work created for this collection, each of which is a response to the question “what is your most beautiful mathematical expression?” These elegant streams of symbols and diagrams serve as mathematical madeleines for moments of discovery and connection, be they between ideas, or people, or both. In those connections our artists (and all mathematicians, computer scientists, and physicists are artists!) find beauty. The Concinnitas project was itself born of a surprising connection between ideas and between people, the result of a chance encounter on an airplane between a mathematician who likes to think about art and an art dealer who likes to think about mathematics. I’m grateful to the many people who helped bring it to fruition—especially to the artists whose work is represented here.
Concinnitas is a collection of ten aquatints produced from the contributions of ten mathematicians and physicists, nearly all affiliated with the Institute, in response to the prompt to transcribe their most beautiful mathematical expression. In October, Robbert Dijkgraaf, Director of the Institute and Leon Levy Professor, moderated a discussion with the portfolio’s curator, Daniel Rockmore, former Member (1995–96, 2002) in the School of Mathematics and Professor of Mathematics at Dartmouth College, and contributors Enrico Bombieri, Professor Emeritus in the School of Mathematics, and Freeman Dyson, Professor Emeritus in the School of Natural Sciences.
This is part of the portfolio and describes the inspiration behind this contribution, which has been exhibited at galleries in Portland, Seattle, and Zurich. The print was produced by Harlan & Weaver, Inc., of New York and published in a series of 100 by Parasol Press, LTD, and the Yale Art Gallery. The print is on exhibit at the Institute and is also in the collection of the Metropolitan Museum of Art.