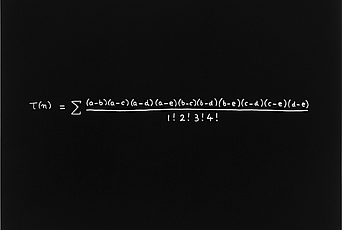The Ree Group Formula

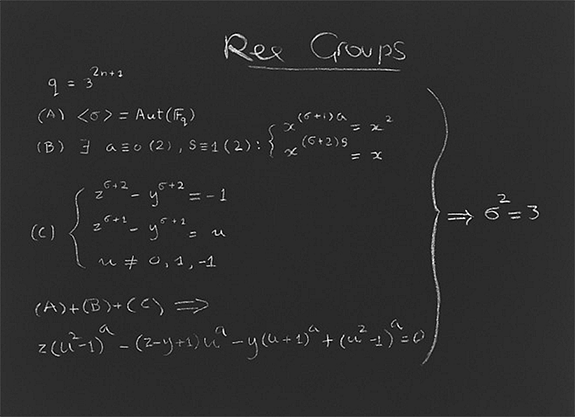
Does beauty exist in mathematics? The question concerns mathematical objects and their relations, the real subject of verifiable proofs. Mathematicians generally agree that beauty does exist in the structural beauty of theorems and proofs, even if most of the time it is largely visible only to mathematicians themselves.

The concept of group beautifully expresses symmetry in mathematics. What is a group? Consider any object, concrete or abstract. A symmetry of the object—mathematically, an automorphism—is a mapping of the object onto itself that preserves all of its properties. The product of two symmetries, one followed by the other, also is a symmetry, and every symmetry has an inverse that undoes it. Mathematicians consider continuous Lie groups, such as the rotations of a circle or of a sphere, to be a beautiful foundation for a great portion of mathematics, and for physics as well. Besides continuous Lie groups there are noncontinuous finite and discrete groups; some are obtainable from Lie groups by reduction to a finite or discrete setting.

Groups can be extremely complicated. Given a group, it may happen that there is a mapping of it to another group, preserving the product structure. A group is simple if the image of such a mapping is always either a copy of the first group or just one element, the identity. Simple groups are the basic building blocks of all groups, so knowing all simple groups is essential in the study of arbitrary groups. General finite groups of symmetries appeared for the first time in the work of É́variste Galois on the subject of algebraic equations. Galois, at the age of only eighteen, was able to prove that the general equation of degree 5 is insoluble by means of algebraic operations by showing that the group A5 of even permutations (that is, permutations consisting of an even number of pair exchanges) on the five letters a,b,c,d,e is a simple group. This group is the smallest non-commutative simple group and also turns out to be the group of symmetries of the icosahedron, a very nice geometry! It was conceivable that simple groups could be described as symmetries of special geometric objects, but the difficulty of studying an abstract, hypothetical, simple group consisted precisely in building a rich geometry out of its internal properties. As of today, the complete proof of the classification theorem that lists all finite simple groups runs over three thousand pages and took over forty years of the collective efforts of more than one hundred mathematicians.

The families of simple finite groups arising from Lie groups were found early, with three exceptions. These families arise by working not over the real or complex numbers, but instead over finite fields of characteristic p, where p is a prime number. There, one can still do the ordinary operations of arithmetic, but multiplication by p always yields 0. Everything went smoothly, if not easily, except for the discovery by the mathematician Ree that the Lie groups B2 and F4 in characteristic 2, and G2 in characteristic 3, also admitted an extra symmetry which could be used to obtain new families of simple groups, nowadays called the twisted Ree groups; the twisted B2 groups and their uniqueness had been obtained earlier by Suzuki using entirely different methods. Uniqueness in the F4 case was also found, but in the G2 case it turned out to be elusive.

After a great effort by Thompson, the uniqueness problem for G2 was reduced to proving that a certain transformation of a finite field of characteristic 3, satisfying a very complicated set of equations in many variables, had the property that its square σ2 on x was the same as the cube x3, in other words σ2=3. Unfortunately, ordinary algebra for eliminating variables quickly led to equations with a number of terms so big that all computers in the world could not store the formulas in their memory banks. What to do? Already in 1973, Thompson got me interested in the problem, but I got nowhere in the maze of formulas. In 1979, when the work on classification was in full swing, I looked again at Thompson’s equations. I asked myself whether was it necessary to write down these “impossible’” formulas, perhaps there was a way around. By a strange trick, it turned out that one small but useful additional piece of information could be extracted from the elimination. By redoing the elimination together with the trick and the new piece of information, the additional information was refined. By repeating three times this refinement process, the sought-for equation σ2=3 was obtained, except possibly for a few cases checkable by computer. Thus the uniqueness problem was solved and another brick was added to the proof of the classification of finite simple groups.

The print is done as a writing in white chalk on a dark slate-blue blackboard, starting at the left with the Thompson equations and with the double arrow pointing to σ2=3, indicating that indeed the equations on the left imply the uniqueness of the twisted Ree groups. The problem was beautiful, the expected answer was also simple, hence beautiful, and the Thompson equations had an inner secret beauty because they reflected the properties of a group. To the expert, the solution obtained by avoiding brute force also had its own beauty. Indeed, mathematicians, sometimes involuntarily, in their search for truth also look for beauty as a guide. As the poet Keats wrote, beauty is truth, truth beauty.

* Thanks to Sarah Jones Nelson