The Macdonald Equation
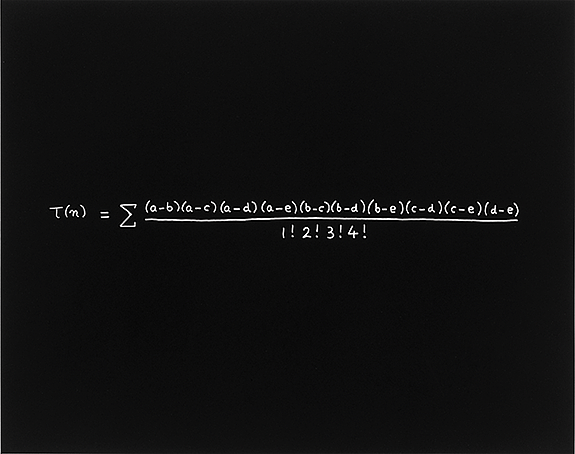
The Macdonald Equation is the most beautiful thing that I ever discovered. It belongs to the theory of numbers, the most useless and ancient branch of mathematics. My friend Ian Macdonald had the joy of discovering it first, and I had the almost equal joy of discovering it second. Neither of us knew that the other was working on it. We had daughters in the same class at school, so we talked about our daughters and not about mathematics. We discovered an equation for the “Tau-function” (written τ(n)), an object explored by the Indian genius Srinivasa Ramanujan four years before he died at age thirty-two. Here I wrote down Macdonald’s equation for the Tau-function. The Macdonald equation has an amazing five-fold symmetry that Ramanujan missed. You can see the five-fold symmetry in the ten differences multiplied together on the right-hand side of the equation. We are grateful to Ramanujan, not only for the many beautiful things that he discovered, but also for the beautiful things that he left for other people to discover.
To explain how the Macdonald equation works, let us look at the first three cases, n=1, 2, 3. The sum is over sets of five integers a, b, c, d, e with sum zero and with the sum of their squares equal to 10n. The “(mod 5)” statement means that a is of the form 5j+1, b is of the form 5k+2, and so on up to e of the form 5p+5, where j, k, and p are positive or negative integers. The exclamation marks in the equation mean 1!=1, 2!=1×2=2, 3!=1×2×3=6, 4!=1×2×3×4=24. So when n=1, the only choice for a, b, c, d, e is 1, 2, -2, -1, 0, and we find tau(1)=1. When n=2, the only choice is 1, –3, 3, –1, 0, and we find tau(2)=–24. When n=3, there are two choices, 1, –3, –2, 4, 0 and –4, 2, 3, –1, 0, which give equal contributions, and we find tau(3)=252. It is easy to check that these three values of tau(n) agree with the values given by Ramanujan’s equation.
The Macdonald equation is a special case of a much deeper connection that Ian Macdonald discovered between two kinds of symmetry which we call modular and affine. The two kinds of symmetry were originally found in separate parts of science, modular in pure mathematics and affine in physics. Modular symmetry is displayed for everyone to see in the drawings of flying angels and devils by the artist Maurits Escher. Escher understood the mathematics and got the details right. Affine symmetry is displayed in the peculiar groupings of particles created by physicists with high-energy accelerators. The mathematician Robert Langlands was the first to conjecture a connection between these and other kinds of symmetry. Ian Macdonald took a big step toward making Langlands’s dream come true. The equation that I wrote down here is a small piece of Macdonald’s big step.
Concinnitas is a collection of ten aquatints produced from the contributions of ten mathematicians and physicists, nearly all affiliated with the Institute, in response to the prompt to transcribe their most beautiful mathematical expression. In October, Robbert Dijkgraaf, Director of the Institute and Leon Levy Professor, moderated a discussion with the portfolio’s curator, Daniel Rockmore, former Member (1995–96, 2002) in the School of Mathematics and Professor of Mathematics at Dartmouth College, and contributors Enrico Bombieri, Professor Emeritus in the School of Mathematics, and Freeman Dyson, Professor Emeritus in the School of Natural Sciences.
This is part of the portfolio and describes the inspiration behind this contribution, which has been exhibited at galleries in Portland, Seattle, and Zurich. The print was produced by Harlan & Weaver, Inc., of New York and published in a series of 100 by Parasol Press, LTD, and the Yale Art Gallery. The print is on exhibit at the Institute and is also in the collection of the Metropolitan Museum of Art.


