Dating the Earth, the Sun, and the Stars

“How big” is almost always an easier question to answer than “how old.” Though we can measure the sizes of animals and plants easily enough, we can often only guess at their ages. The same was long true of the cosmos. The ancient Greeks Eratosthenes and Aristarchus measured the size of the Earth and Moon, but could not begin to understand how old they were. With space telescopes, we can now even measure the distances to stars thousands of light-years away using parallax, the same geometric technique proposed by Aristarchus, but no new technology can overcome the fundamental mismatch between the human lifespan and the timescales of the Earth, stars, and universe itself. Despite this, we now know the ages of the Earth and the universe to much better than 1 percent, and are beginning to date individual stars. Our ability to measure ages, to place ourselves in time as well as in space, stands as one of the greatest achievements of the last one hundred years.
In the Western world, the key to the age of the Earth was long assumed to be the Bible and its account of creation. Creation dating required careful accounting of the chronology given in Genesis and then matching it to historical events recorded elsewhere. Though James Ussher’s date of 4004 B.C.E. is the most famous result (and is still accepted by many Biblical literalists), scientists and theologians including Maimonides, Isaac Newton, and Johannes Kepler also worked out dates around 4000 B.C.E. These estimates were not seriously challenged until the emergence of modern geology in the eighteenth century.
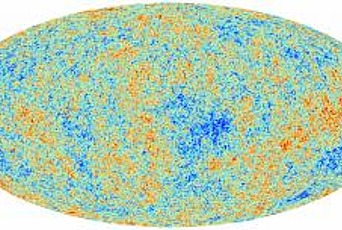
In the mid-1700s, the Scottish geologist James Hutton proposed that the processes of erosion, sedimentation, and volcanism that we observe today happened much the same way in the past. Acting over many millions of years, they could explain the geological record without recourse to the great flood of Noah. Charles Lyell popularized the concept of uniformitarianism in the mid-1800s and argued that the Earth had to be very old indeed. More generally, uniformitarianism holds that the physical laws and processes we see today are the key to understanding the past. This is the idea that, today, enables scientists (including many past and present Members of the Institute) to understand the afterglow of the Big Bang and to see the universe as it was 380,000 years after it formed.
Astrophysics first had something to add to the question of ages with the discovery of thermodynamics in the late 1800s. The gradual contraction of the Sun due to gravity could be a source of energy, replenishing the energy radiated away by sunshine. The Sun must be shrinking for this explanation to work. Turn the clock backwards, and at some point, the Sun must have extended past Earth’s orbit. Lord Kelvin calculated that the Sun could only have sustained its current luminosity for about 20–40 million years. This was much too short for the geologists. It remained a puzzle until the discovery of nuclear fusion, the Sun’s actual energy source, in the 1930s.
It was also astrophysics that finally provided a method for dating the Earth itself. In the early twentieth century, it was discovered that some chemical elements decay into others at highly stable rates. By measuring these rates, and the relative amounts of parent and daughter atoms in a rock, scientists could measure how long it had been since the rock solidified. The problem was that even the oldest rocks were not as old as the Earth itself. The young Earth was a hot and violent place, and even now, the Earth’s surface is constantly changing as rocks are deposited, eroded away, and subducted into the mantle. The solution lay in space, where asteroids have remained essentially unchanged since the formation of the solar system. In 1953, Clair Cameron Patterson measured the abundances of three isotopes of lead in meteorites and calculated that the Earth must be about 4.6 billion years old. Small uncertainties in this number exist not because of any shortcomings of radioactive dating, but because we do not know the exact order in which the solar system formed. We can measure the ages of tiny grains in meteorites, called chondrules, to just 100,000 years out of 4.6 billion.
The measurement of the age of the universe is a similar triumph. It began with Edwin Hubble’s discovery that galaxies are all flying away from one another. If galaxies are flying apart now, they must have been closer together in the past, and we can keep turning the clock back until all galaxies lay on top of one another. The universe at this time would have been incredibly hot and dense, bathed in radiation that could still be seen today. The discovery of this background radiation in the 1960s was strong evidence for a beginning (a Big Bang). Its detailed study in the last two decades, with major contributions from past and present Members of the Institute, has enabled us to determine the age of the universe to incredible precision: 13.8 billion years, give or take 40 million, an error of just 0.3 percent.
While we know the age of the Sun to about 0.1 percent, this is not true of any other star. It would not even be true of our Sun without meteoritic dating. Stars change little over billions of years: the Sun would have looked much the same to the dinosaurs as it does to us. However slowly though, stars do evolve. As the Sun’s core converts hydrogen into the heavier element helium, its temperature increases to maintain the pressure needed to balance the crushing force of gravity. The same physics applies to balloons: filling a balloon with helium will keep it aloft, but switch out the helium for the same mass of heavier air molecules and you need a heater to keep it in the air (a hot-air balloon). The rate of nuclear reactions goes up as the core temperature rises, and the Sun shines more brightly. It is about 30 percent brighter today than when the Earth was young. This slow change in a star’s temperature and brightness provides a clue, for many stars the only clue, to its age.
We estimate the ages of stars by simulating them on a computer and trying to match their properties to those of the stars we see. We take a star’s worth of gas held together by gravity, calculate its structure, and then follow its evolution over millions or billions of years. The process relies on a lot of measurements and simplifying assumptions—from the temperature-dependent rates of many different nuclear reactions, to the absorbing and emitting properties of atoms under temperatures and pressures inaccessible on Earth, to the treatment of convection and rotation in the stellar interior. A full three-dimensional simulation of a star over its entire lifetime is well beyond the reach of any supercomputer. Perhaps surprisingly, the physics of the early universe is much simpler than the physics of a stellar interior, which is one reason why we can know the universe’s basic properties to such precision.
The basic picture of stellar evolution was worked out decades ago: stars use up their hydrogen fuel, their cores contract and heat up, and sufficiently massive stars can fuse the helium into heavier and heavier elements. Eventually, either a star cannot attain the temperatures and pressures needed to fuse the next element, or it has fused all the way to iron (the most stable element) and cannot extract any more nuclear energy. The stellar core becomes a compact remnant (a white dwarf, neutron star, or black hole), and its outer layers either drift off into space or are thrown off violently in a supernova. The lifetime and fate of a star depend mostly on its mass, with massive stars living short lives, shining brightly, and dying in supernovae.
While the outline of stellar evolution is clear, it is the details that matter for stellar ages. Advances are made with careful improvements to stellar modeling, and typically make small differences in the results. Occasionally, though, it becomes possible to model an important physical effect that was previously neglected. This is now the case with stellar rotation. Rotation breaks a star’s spherical symmetry (making the problem much more computationally challenging), but it also helps to support the stars against gravity, and can mix huge amounts of extra fuel into the core. Rotating stars burn more hydrogen over their lives; they live longer and shine brighter than their nonrotating counterparts. Rotating stellar models are forcing us to reconsider the ages of nearby star clusters, making them as much as 25 percent older than had been thought. These cluster ages are often used to anchor other dating techniques. Revising them could lead to a sort of domino effect, where many physical processes happen a bit more slowly than we had thought.
More intriguingly, stellar rotation may also explain a recent puzzle. Some star clusters seem to show a range of several hundred million years in age, much longer than standard star formation theory predicts. Just a few million years after forming, the most massive stars in a cluster end their lives as powerful supernova explosions, blowing away the remaining interstellar gas and cutting off star formation. Stellar rotation provides a simple solution: rotating stars can mix more fuel into their cores, increasing their supply of available energy and slowing the stellar aging process. These clusters have a range not of ages, but of aging rates. The effect is even stronger when considering that rapid rotation flattens a star. The poles of a rotating star are hotter than the equator; someone viewing the star pole-on will see a higher temperature and a larger area. Vega, one of the brightest stars in the night sky, is a very rapid rotator seen nearly pole-on. Viewed edge-on, Vega would only appear to be half as bright. A population of Vega clones oriented in all directions would show a wide range of apparent temperatures and luminosities, exactly the properties that we use to infer ages.
As stellar models continue to improve, a new tool has begun to offer a window into stellar interiors. Our best data on the interior of the Earth comes from measuring vibrations, from earthquakes to waves crashing on a shore, as they travel through rock, mantle, and core. These waves propagate differently depending on the material and allow us to peer inside the Earth. The same thing happens in stars, where convection and mixing stir up the stellar interior, which vibrates in response. We can detect these vibrations as tiny fluctuations in brightness produced by waves on the stellar surface. By measuring their frequencies, we learn about the conditions deep in the stellar interior.
The Kepler satellite is famous for detecting thousands of exoplanets by their transits across the faces of their host stars. Arguably just as important, however, are Kepler’s measurements of starquakes on thousands of stars. These have allowed us to probe far below the stellar surface, into the cores where hydrogen fuses into helium over billions of years. The composition of the core tells us how much hydrogen has been burned, while the amount of starlight tells us how fast the core must be using up its nuclear fuel. Kepler has now brought the former measurement within reach. We build space telescopes like Kepler and its successor TESS mostly to find planets. But thanks to these missions, it may soon be possible to know the age of almost any bright star in the sky.