Hot Topic: Arithmetic Combinatorics

During the first term of 2007–08, School of Mathematics Professor Jean Bourgain and Member Van Vu of Rutgers, The State University of New Jersey, ran a program on arithmetic combinatorics. The Members in residence for the program ranged from Endre Szemerédi, one of the fathers of the subject, to Ben Green, a young leader in the field, and included five recently graduated postdocs. Combinatorics is concerned with counting problems. The theorems in the subject typically do not assume much structure and apply quite generally. Arithmetic is concerned with algebraic operations on the integers or in mathematical structures, called finite fields, and is usually a very structured study. There have been a number of striking results proved in recent years, which are based on the interplay between arithmetic and combinatorics and this has resulted in a flurry of activity. This was the reason that the topic was added to the year-long program on new connections of representation theory to algebraic geometry and physics, as a second short program.
An example of a basic and powerful theorem in arithmetic combinatorics is the sum product theorem of Bourgain, Nets Katz, and Terence Tao. It is an elementary but fundamental quantitative combinatorial fact about the way addition and multiplication work in finite sets of integers (stated precisely below). Given its basic nature, it is not surprising that it and its generalizations have wide applications to algebra, number theory, theoretical computer science, and most recently to group theory.
Many of these striking applications were presented in the seminars and mini-courses during the term. These included the proof by Bourgain and Alexander Gamburd of Alex Lubotzky’s expanders in finite groups conjecture and the work by Harald Helfgott, which opened the door to this development. Members Gamburd and Helfgott were among the many experts who were present for the term. For some years now, expanders have been a popular topic in the School with Herbert H. Maass Professor Avi Wigderson and Visiting Professor Noga Alon applying them to problems in combinatorics and complexity and Professor Peter Sarnak to problems in number theory.
Another very interesting subject, central to the program, was the application of combinatorial methods to the proofs of theorems about arithmetic progressions in sets of integers and similar results about primes. An example of such an application is the Green-Tao theorem, which states that the prime numbers contain arbitrary long arithmetic progressions. [For example, 5, 11, 17, 23, 29 is a sequence of five primes equally spaced, and so in arithmetic progression, the Green-Tao theorem says that you can find sequences of equally spaced primes which are as long as you like, though the spacing between them might be bigger.]
A third very active topic in arithmetic combinatorics is the study of discrete random matrices of large size. Van Vu’s minicourse explained a number of the striking recent advances, some of which were also presented by Visitors and Members in the weekly seminar. A survey of these developments can be found in Tao’s Milliman Lectures.
The weekly seminars on Tuesday afternoons were especially well attended and elicited lively discussions about varied applications of new breakthroughs, a number of which were made during the term. To end the program Bourgain, Sarnak, and Vu ran a three-day mini-conference. It drew Members involved in the program as well as many experts who traveled to the conference.
Sum Product Theorem
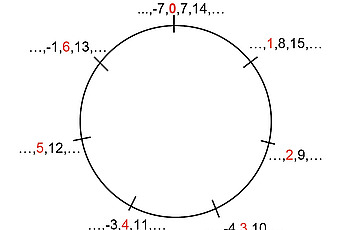
If p is a prime number, we can define addition and multiplication of the numbers {0,1,2, . . . , p –1} by the usual processes of addition and multiplication but taking the remainder when the answer is divided by p. The numbers {0, 1, 2, . . . , p –1} with addition and multiplication defined like this constitute what is called the finite field Fp. If e is any positive number, the theorem states that we can find another positive number d such that, for large enough prime numbers p, and for any subset A of the p integers Fp, with at most p1– e elements, either the number of elements in A.A or the number of elements in A+A is larger than |A|1+d. Here A.A is the set of all products x.y, and A+A is the set of all sums x+y, where x, y are any integers in Fp, and |A| is the number of elements in A.