Dynamics in Translation

Should you ever deign to leave the Institute campus and head a few miles north along Route 1, you will arrive at another world leading facility: the Princeton Plasma Physics Laboratory (PPPL). The Laboratory sprang out of Cold War attempts to control thermonuclear reactions, but since 1951 has been at the heart of U.S. efforts to produce clean energy and ultimately save the planet. Its mission is to develop nuclear fusion as a sustainable energy source, which, if successful, would end our reliance on fossil fuels. 

More specifically, fusion scientists are attempting to harness the power latent in plasma. Plasma is a fourth state of matter—distinct from solids, liquids, and gases—which can be produced by heating gas to such high temperatures that the electrically neutral atoms comprising it are ripped into their constituent parts: negatively charged electrons and positively charged nuclei, known as ions. Fusion physicists at PPPL inject these electrons and ions into a donut-shaped device known as a tokamak, and then attempt to control their motion using electromagnetic fields. Their aim is to force the ions to collide with each other at high speed and fuse. It is this fusion process that releases excess energy which can then be harnessed outside of the device. 

While the practices of the fusion physicists at PPPL may seem completely divorced from the realm of theoretical astrophysics, they are now a regular topic of discussion among the scholars of the Institute’s School of Natural Sciences. The reason for this has nothing to do with atomic energy. Instead, it turns out that the mathematical methods developed to exploit the power of the electrons, ions, and magnetic fields in fusion plasmas are precisely the same as those needed to describe the dynamics of stars, spiral arms, and dark matter in galaxies like the Milky Way. 

The fields of plasma physics and galactic dynamics are divided by a thick fog of complex jargon and obscure practice, but once one has become fluent in both Plasmish and Galacticese, and has developed a dictionary relating the two, one can pull ideas directly from one field to solve a problem in the other.  

Wave-particle interactions, Landau damping, and LBK 

That plasma physics and galactic dynamics are intellectually adjacent is not a new discovery. In the 1940s and 1950s, Lyman Spitzer, a founding member of both PPPL and Princeton University’s Astrophysical Sciences division, was a reigning master of both fields. In 1972, two past IAS Members in the School of Natural Sciences, Donald Lynden-Bell (2003) and Agris Kalnajs (1979–80), drew extensively on plasma theory to write what I consider to be the greatest paper to date in the field of galactic dynamics: On the generating mechanism of spiral structure.¹ Lynden-Bell and Kalnajs’s work will be relevant throughout this article, so as a shorthand, I’ll refer to them as LBK. 

I’m going to explain just one small part of what LBK showed in their 1972 masterpiece, but first I need to tell you about the fundamental plasma theory that inspired them, namely Landau damping.² This is something that still fascinates mathematicians and physicists today. In fact, Cédric Villani, past Member in the School of Mathematics (2009), was awarded the 2010 Fields Medal partly for his work on this subject, much of which was completed at IAS. 

The best way to understand Landau damping is to take a rather macabre approach. Imagine you are trapped inside a plasma and are desperately shouting for help. Since the plasma medium consists of charged particles, the sound wave produced by your scream (technically known as an ion-acoustic wave) would carry its own electric field, whose value is indicated on the vertical axis in Figure 1. The sound wave moves in time from left to right along the x-axis. Supposing your rescuers are situated somewhere along the x-axis, you might hope that your sound wave will reach them before too long.

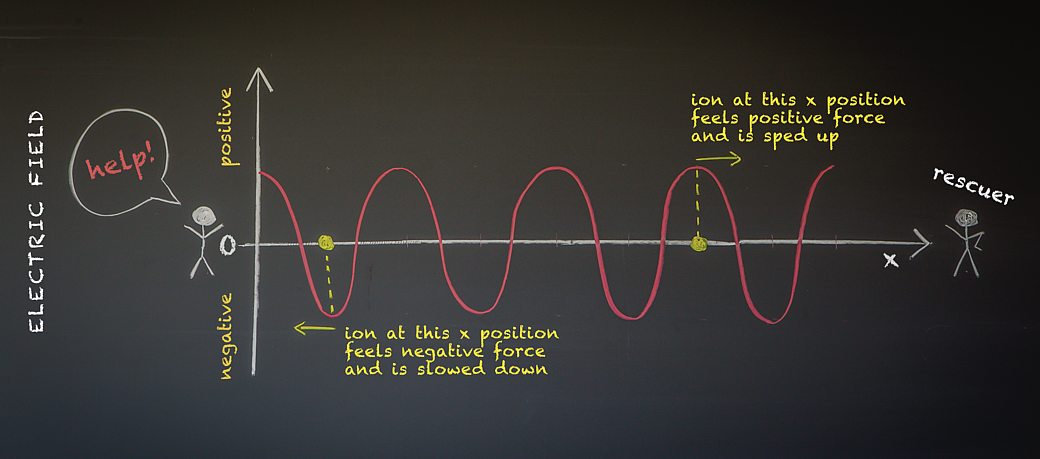
But there’s a problem. Your sound wave would also interact with other particles within the plasma, such as positively charged ions, which will also be moving along the x-axis. At a fixed time, if an ion is located along the x-axis at a position where the wave’s electric field is negative, then it experiences an opposing force from the wave in the x direction, slowing it down. Conversely, if an ion is located at a position where the wave’s electric field is positive, it feels a further push from the wave, speeding it up. The total energy of the wave-particle system must be conserved. Thus, if the wave happens to cause the ion to speed up, the energy required to do this must be sucked out of the wave, meaning that the wave decays in amplitude, or damps.

For the vast majority of ions, the force that they feel from the wave will sometimes be positive, sometimes negative, and these pushes and pulls will typically cancel each other out. As a result, there will be, on average, no energy transfer between wave and ion, and so no net wave damping will occur. But Landau understood that this is not the case for all ions. Instead, a small fraction of the ions resonate with the wave, which means that they move along the x-axis at very nearly the same speed as the wave does. For these select few resonant ions, the aforementioned cancelling-out never occurs. In fact, Landau showed that for the resonant ions, the overall force they typically feel from the wave is net positive; i.e., on average these ions speed up. Due to energy conservation, the overall force on the wave is, therefore, negative, causing it to decay in amplitude, or Landau damp. One consequence of Landau’s result is that it can be very difficult to propagate a sound wave through a plasma; or, to put it more dramatically, in plasma, no one can hear you scream.

Back to gravity. LBK looked at the mechanism of Landau damping and realized that it also applied to astrophysical systems. Their analysis showed that Landau’s mechanism describing the interaction of sound waves, and ions in a plasma can also be used to investigate the evolution of a galaxy’s bar.

A bar is an elongated agglomeration of millions of stars which exists at the center of a galaxy (Figure 2). Such bars are common in disk-shaped galaxies, including our own, the Milky Way. A bar does not sit inert, but rather rotates around its middle as if it were a solid body, like a gigantic stirring spoon being twirled at the center of a galactic latte. LBK showed that the bar’s gravitational field in the galaxy is entirely analogous to the electric field in plasma, and this gravity field interacts with stars and other objects orbiting in the galaxy, just as the electric field interacts with ions. These interactions cause energy to be transferred to and from the bar, which in turn causes the bar to spin faster or slower. In other words, LBK’s theory allows us to understand the spin of bars by treating a galaxy as if it were a gravitational plasma.³

The problem with galactic bars

Much of my work at the Institute has also focused on leveraging classic plasma results to solve analogous astrophysical problems. One of the papers of which I am most proud was written alongside my IAS School of Natural Sciences colleagues Elizabeth Tolman (Member, 2020–22) and Lev Arzamasskiy (Member, 2020–23), as well as Vinicius Duarte, a research scientist at PPPL.⁴ Now, prior to this project, none of my coauthors had worked on galactic dynamics, and Duarte had never studied astrophysics at all. But I knew they were much more fluent than me in the language of theoretical plasma physics. Thus, they were galactic dynamicists already; they just didn’t know it yet.

The problem I wished to address concerned the evolution of galactic bars. The central issue—and one that has caused much controversy in the astrophysical community in recent years—is that these bars seem to be spinning too fast.

When I say ‘too fast,’ I mean that the bars we observe in thousands of galaxies external to our own are rotating too rapidly compared to the predictions of our standard cosmological theory. This is the theory of dark matter—that mysterious and bewildering stuff whose gravitational imprints are rife throughout the universe but which has, so far, eluded our direct capture.

Dark-matter-based cosmology theory tells us that each galaxy is surrounded by a massive, roughly spherical halo of dark matter particles (Figure 3). These particles orbit around the galaxy, and interact gravitationally with the spinning bar. Following Landau and LBK, we expect that the dark matter particles that resonate with the bar (i.e., those which orbit the galaxy at the same rate that the bar spins) will suck energy out of it. In other words, trying to spin a stellar bar inside a deep gravitational well of dark matter should be like twirling your coffee stirrer through molasses. Indeed, applying the LBK equations to this problem shows that the spin rate of bars ought to decrease dramatically within the lifetime of the galaxy. This conclusion is corroborated by computer simulations of galaxies surrounded by dark matter haloes: in many of those too, the bars slow down. 

Yet the bars that astronomers observe today are spinning fast! This has led some physicists to claim that standard cosmology is in crisis, and that perhaps the dark matter theory should be abandoned altogether.

A partial solution to this problem comes from 1984, when IAS Professor Emeritus Scott Tremaine and Martin Weinberg, past Member (1987–90, 2010) in the School of Natural Sciences, published an update to the LBK theory, which we’ll call the TW theory.⁵ In particular, TW accounted for the fact that dark matter particles can become ‘trapped’ in the gravitational field of the bar and dragged along with it. The stronger the gravitational field of the bar is, the more dark matter can be trapped. Further, TW showed that trapped particles do not give or take energy from the bar on average. Thus, when many particles are trapped, the bar will continue to spin fast, and the slowdown predicted by LBK can be avoided.

However, both the LBK and TW theories ignore the fact that, in reality, dark matter particles are not only influenced by the gravity of the bar. That’s because real galaxies are messy machines: they also comprise molecular gas clouds, star clusters, spiral arms, and various other bits and pieces of galactic shrapnel which shuffle and nudge the dark matter particles in their vicinity in a process known as diffusion. I wondered: how are the classic LBK and TW results modified if one includes this inevitable diffusion? In fact, do these analytic theories provide any insight into the real problem whatsoever?

Our contribution

It turns out that the aforementioned questions had already been tackled in—you guessed it—plasma physics; more precisely, in the theory of plasma fusion in tokamaks. In plasma physics, it is well understood that resonant interactions between magnetic waves and energetic ions can be interrupted when the ions collide with the background plasma particles and are knocked off course.⁶ Several tokamak scientists, including Tolman and Duarte, had previously studied how magnetic wave-particle interactions are modified by this so-called collisional diffusion.

Our insight, therefore, was that a galaxy is a kind of gravitational tokamak. We showed that in a galaxy with diffusion artificially set to zero, the general bar-dark matter halo interaction will eventually lead to zero slowdown of the bar, just as TW predicted. But as one adds in even a very small amount of diffusion, the interaction is modified, and the bar’s slowdown rate increases dramatically, until eventually it reaches the value predicted by LBK.⁷ Thus one can think of TW and LBK as two ends of a spectrum, describing the cases with ‘zero diffusion’ and ‘lots of diffusion,’ respectively (even though neither TW nor LBK considered diffusion explicitly).

Next, using the known properties of observed galaxies, we estimated that most bars in the real universe probably sit quite close to the ‘zero diffusion’ limit. Therefore, they are approximately described by TW theory, which can explain why most of them are spinning rapidly. On the other hand, we also estimated that in computer simulations of those same galaxies, there is significantly enhanced diffusion. (This artificial diffusion is an inevitable consequence of simulating a hugely complex system with finite computational resources.) This means that the galaxies being simulated on the computer are not well described by the TW theory. Instead, their extra spurious diffusion puts them closer to the LBK limit. Since LBK predicts slowdown where TW does not, it is natural that the bars in real galaxies would be spinning more rapidly than those in simulations thereof.

Having said this, we cannot claim to have solved the problem of fast-spinning bars. Even though our model is somewhat more sophisticated than the classic works of LBK and TW, it is still a drastically simplified version of a real galaxy, and there are many important effects we did not account for. But by isolating the effect of diffusion, and lifting analogous results from tokamak fusion theory, we were able to gain insight into the bar-halo interaction, and learn something that a brute-force computational experiment might never have revealed.

What’s next?

Kleptomania is a bad habit. But I must admit that since the bar-halo project I have continued to co-opt ideas from plasma physics for my own purposes. I have used such ideas to study the strength of galactic spiral arms, to understand the response of barely-stable stellar systems to gravitational perturbations, and to probe the strange orbital distributions of wide binary stars in the Milky Way.

In the future, I hope that the plasma-galactic relationship flourishes in a symbiotic, and not a parasitic, fashion. After all, plasma physicists can also learn from us. Lynden-Bell’s famous theory of violent galactic relaxation is these days a mainstay of plasma theory. Villani’s work was partly inspired by the discussions of gravitational Landau damping in the bible of my subject, Galactic Dynamics by Binney and Tremaine. And with our bar-halo work, we inadvertently provided the most detailed and general study of resonant wave-particle interactions in the presence of diffusion to date, something that can be reclaimed by the plasma theorists and applied in whatever context they see fit.

I cannot predict the outcome of our continuing efforts in reconnecting the plasma and galactic communities, but I do know that therein lies fertile ground. If fusion is one day successful, perhaps our silly study of bars and galaxies will have played a tiny role in saving the planet. Now, whoever said astrophysics isn’t useful?

Chris Hamilton is a John N. Bahcall Fellow in the School of Natural Sciences. He moved to the Institute in 2021, after completing his Ph.D. at the University of Cambridge, for which he was awarded the International Astronomical Union’s Ph.D. Prize. His interests include black hole mergers and the gravitational dynamics of galaxies, globular clusters, binary stars, and planetary systems. He also delivers an annual lecture course on the kinetic theory of stellar systems to Masters students at the University of Oxford.