Black Holes as Laboratories

Black holes are fascinating objects that capture the imagination of the general public and scientists alike. And yet, they are remarkably simple. According to Einstein’s theory of gravity—general relativity—black holes can be fully described by only three basic parameters: mass, angular momentum, and electric charge. Unlike most objects we commonly encounter, black holes of all masses have the same fundamental shape (or geometry), given the same spin and electric charge. A more massive black hole will have the same geometry as a less massive one, but scaled up in size. It is, therefore, no surprise that the first image of the black hole at the center of our own galaxy, published on May 12, 2022 by the Event Horizon Telescope (EHT) Collaboration, seems remarkably familiar.1
The now famous “orange donut” image of the black hole at the center of the M87 galaxy was first published by the EHT in April of 2019. The black hole at the center of our galaxy, called Sagittarius A* (Sgr A*)— revealed in May 2022—is approximately 1,500 times less massive than the black hole in the M87 galaxy. It’s also about 2,000 times closer to Earth, which results in an “orange donut” of similar size from our point of view. The fact that the two black hole images look so similar—both with a ring of emission (the bright donut) and a central brightness depression (the empty donut hole)—is a remarkable confirmation of general relativity. These two black hole images, together with gravitational wave detections, show that black holes of vastly different masses are all consistent with the predictions of Einstein’s theory. The unparalleled resolution of the EHT images allows us to use black holes in space to test assumptions, predictions, and alternatives—bringing to the fore an era of astrophysics where astrophysical black holes can finally be used as laboratories to test our understanding of gravity itself.
Why Use Black Holes as Laboratories?
Einstein developed the theory of general relativity between 1907 and 1915. According to his theory, what we experience as gravity is actually a geometric effect— mass tells spacetime how to curve, and the curvature of spacetime in turn tells mass how to move. The orbits of the planets are not caused by the gravitational “pull” of the sun, but rather, the mass of the sun curves the spacetime around it. The planets are trying to move in straight lines but are unable to, due to the curvature of the space they are moving through. General relativity was first tested over 100 years ago and since then has been tested numerous times, with, for example, pulsar observations, cosmological studies, and measurements within the solar system. One might wonder, then, why we still test this theory, when it has already been tested for over a century. When testing a fundamental theory, it is important to keep in mind that validating one prediction of the theory does not guarantee that other predictions will also hold. For example, Newtonian mechanics had passed many tests before general relativity was developed, but we now know that, while Newtonian mechanics is a great approximation in many cases, it is not complete. In particular, it is important to test theories in different regimes. For gravity, this means performing tests in very weak gravitational fields (low curvature)—such as tests at large cosmological scales—as well as in incredibly strong gravitational fields (high curvature)— such as tests with black holes. The first detection of gravitational waves from merging black holes by LIGO in 2016 provided the first strong-field test of general relativity. The EHT’s images of M87 and Sgr A* provide new tests in the strong-field regime.
Tests with black hole images are complementary to those with gravitational waves; the latter are primarily sensitive to the dynamical aspects of the theory, while the former are sensitive to the geometry of the black hole itself. The black holes observed in the detection of gravitational waves have masses on the order of tens-oftimes the sun’s mass, while Sgr A* and the black hole in M87 have masses on the order of one-million- and one- billion- times the mass of the sun respectively. Although both tests probe the curvature of spacetime very close to a black hole, the curvature around a small black hole is much higher than that around a large black hole (curvature scales as inverse of mass squared). This means that these black holes can each be used as a laboratory to test general relativity at vastly different curvatures.
Testing with Sgr A* and M87
If general relativity is correct, and if a few physically motivated assumptions hold, then astrophysical black holes must be consistent with a very specific geometry. This specific black hole can rotate (can have spin), but does not have a significant electric charge.2 This spinning but chargeless black hole is called “Kerr,” after Roy Kerr who discovered its geometry in 1963. If we f ind that black holes in space are inconsistent with the Kerr geometry, then either general relativity is incomplete, or one of our physically motivated assumptions is violated. In particular, a violation of Kerr would likely violate the “No Hair Theorem,” which, in colloquial terms, states that a black hole is completely determined by only three numbers: its mass, spin, and charge. A violation of the No Hair Theorem would have important implications for our understanding of gravity.
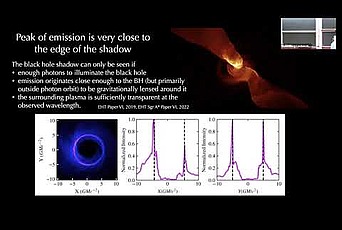
In the recent EHT publications on Sgr A*3 we use the measured size of the ring of emission in the image of Sgr A* to show that this black hole is consistent with the Kerr geometry, as well as to place constraints on alternative geometries. To do this, we calibrate the measurement of the size of the observed ring of emission to the size of the black hole shadow.4 The boundary of the black hole shadow is defined as the critical impact parameter between light-ray trajectories that fall into the black hole and those that escape to infinity, as seen by a distant observer. The black hole curves spacetime and the light rays trace out curved paths through the curved space. Because of this, photons that originally were not directed at the black hole can be curved towards it and fall into the event horizon. Due to the curved trajectories of light rays, the black hole shadow, as seen by a distant observer, will be approximately 2.6 times larger than the event horizon of the black hole. The Kerr geometry predicts a specific shape and size for the black hole shadow, which depend only weakly on the spin of the black hole.
Both Sgr A* and the black hole in the center of the M87 galaxy have very low accretion rates, meaning that a small amount of mass is falling into these black holes relative to their total mass. Due to these low accretion rates, theoretical models predict that the accretion disks around these black holes will be thick—more like a donut than a disk. For such models, the ring of emission in black hole images at short radio wavelengths (i.e., the wavelength at which the EHT observes) coincides with the black hole shadow. In the new EHT results, we use hundreds of thousands of models and simulations to calibrate between the black hole shadow and the ring of emission we observe in the EHT images. The size of the ring of emission seen in the EHT image of Sgr A* is completely consistent with the predictions for a Kerr black hole, and we can measure the size of the black hole shadow with an uncertainty of about ten percent. We consider several geometries that deviate from Kerr in a parametric manner, as well as geometries that are solutions to specific alternative theories. We even consider geometries that are frequently in the realm of science fiction, such as wormholes. Our ten-percent error bound is able to completely rule out several geometries (including a wormhole), and constrain the free parameters of several others.
Testing Whether Sgr A* Has an Event Horizon
One of the most iconic features of a black hole is its event horizon, sometimes referred to as “the point of no return.” The event horizon is not a material surface but rather a mathematically defined boundary. Anything that comes closer to the black hole than this distance can never escape the black hole, not even light itself. The event horizon is crucial to our understanding of black holes, as it censors the singularity from the rest of the universe, avoiding possible unphysical phenomena; one such example of unphysical phenomena predicted around some theoretical naked singularities (singularities not shielded by an event horizon) is the possibility of walking in a circle and running into yourself from a few minutes ago.
Although most physicists and astrophysicists were already confident before the recent EHT observations that Sgr A* was in fact a black hole (and should, therefore, have an event horizon), it is still compelling to directly rule out alternatives. The first alternative is an object with a surface outside of the event horizon and in thermodynamic equilibrium, which absorbs and is heated by incident radiation, and which then re-emits the energy thermally. This model has been developed in the literature for several years; however, one of its free parameters is the size of the emitting region, and the new EHT results provide very stringent constraints on this. The model is further constrained by the measured accretion rate onto Sgr A*, also measured by the EHT. Lastly, this thermal model predicts a significant increase in infrared flux, which is inconsistent with previous infrared observations of Sgr A*. We therefore rule out a thermally emitting surface for Sgr A*.
The second alternative we consider is a surface (outside of the event horizon) that reflects incident radiation. The EHT observations are uniquely suited to constrain such an alternative, since a reflective surface results in additional emission within the center of the ring of emission. Although our exploration of this model is not as extensive as the thermal model discussed above, the depth of the brightness depression in EHT images of Sgr A* can already rule out a completely reflective surface, as well as place constraints on partially reflective surfaces.
Finally, a naked singularity is also a potential alternative to an event horizon, and we consider several examples of naked singularities. Some naked singularities can be completely ruled out or constrained by the measured size of the black hole shadow. However, despite the remarkable high-resolution image, some naked singularities are still able to mimic the expectations of a Kerr black hole and cannot be ruled out. Although these new EHT results have proven very powerful in ruling out several alternatives to an event horizon and, therefore, significantly increased our confidence that event horizons enshroud singularities in space, we cannot conclusively reject all alternatives to an event horizon.
The Future of Testing with Black Holes Strong-field tests of gravity—those with gravitational waves and those with black hole shadows—are com plementary to each other, probing vastly different masses, and, therefore, curvature scales. We can directly compare the constraints between the two experiments and show that, since we are probing very similar gravitational radii, we can achieve comparable constraints on deviations. Before the publication of the first detection of gravitational waves in 2016, there was not a single test of general relativity in the strong-field regime. Only a few years later, we now have several strong-field tests that span over 10 orders of magnitude in black hole mass. This is still only the beginning.
The future looks bright for black hole astrophysics, both for tests with black hole shadows and tests with gravitational waves. In fact, the next generation of gravitational wave detectors are already being planned. Two such instruments, the Einstein Telescope and LISA, will provide a higher rate of detections (due to improved sensitivity) and probe different mass scales. The 2017 observations with the EHT were unprecedented as they were the first very long baseline interferometry observations with a global array. Since then, the EHT has successfully observed targets in 2018, 2021, and 2022 with additional telescopes which have significantly improved image fidelity and modeling constraints. All gravitational tests published by the EHT thus far have used only the size of the emission ring and not its shape. Due to the limited number of telescopes used, the 2017 observations do not provide a strong constraint on the shape of the ring. However, with 2022 data, constraints on the asymmetry of the shape of the ring may finally be possible, which would lead to a new constraint on a different part of the Kerr metric.
Observations at a shorter wavelength are also planned for 2023. Since the resolution scales with wavelength, a shorter wavelength will result in significantly improved resolution. Coupled with the improvements in our observational capabilities, new imaging and model f itting algorithms are continuously being developed. Advancements in analysis methods will further improve constraints on the size and shape of the black hole shadow, and depth of the flux depression resulting in further constraints on alternative geometries, as well as alternatives to an event horizon. With these advancements, astrophysical black holes will become better and better laboratories, providing greater insights into our fundamental theories.
Lia Medeiros is an NSF Astronomy and Astrophysics Postdoctoral Fellow and has been a Member of the School of Natural Sciences since 2019. She is an active member of the EHT collaboration and has held key leadership roles. She is currently developing a new algorithm for EHT data analysis, based on machine learning techniques that use a large high- fidelity simulation library as a training set. In addition to her research, she leads an outreach and education initiative teaching astronomy to students in Princeton High School’s English Language Learners program—many of whom recently immigrated from Guatemala.
- The images of these two black holes, in addition to their geometry, are also affected by the details of the accretion flows around them. Both of these black holes are in the same accretion regime, resulting in very similar images.
- Black holes in space are not expected to have significant electric charge, since they should be able to attract the opposite charge and neutralize themselves.
- The Event Horizon Telescope Collaboration et al 2019 ApJL 875 L6 https://doi.org/10.3847/2041-8213/ab1141.
- The black hole shadow has a precise mathematical definition that depends only on the geometry of the black hole itself, and not on what is happening to the matter around the black hole.