The Strange Behavior of Sound Through Solids

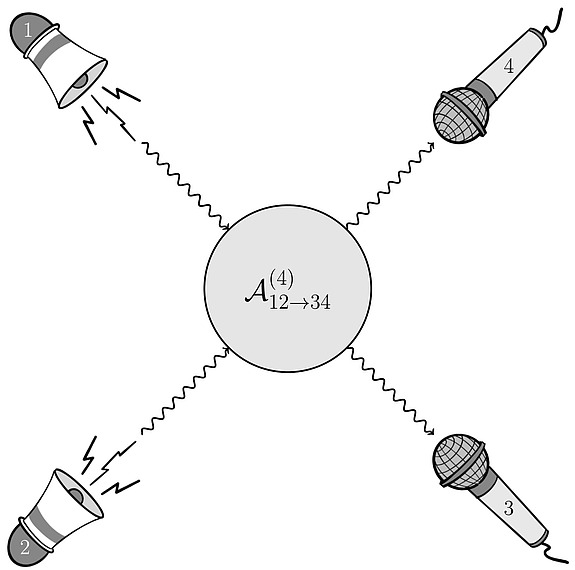
Not everything needs to be seen to be believed; certain things are more readily heard, like a train approaching its station. In a recent paper, published in Physical Review Letters, researchers have put their ears to the rail, discovering a new property of scattering amplitudes based on their study of sound waves through solid matter.

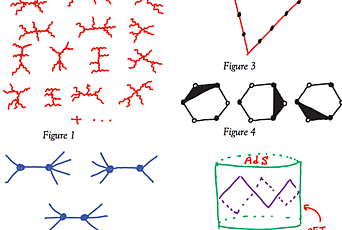
Be it light or sound, physicists consider the likelihood of particle interactions (yes, sound can behave like a particle) in terms of probability curves or scattering amplitudes. It is common lore that, when the momentum or energy of one of the scattered particles goes to zero, scattering amplitudes should always scale with integer powers of momentum (i.e., p¹, p², p³, etc.). What the research team found however, was that the amplitude can be proportional to a fractional power (i.e., p^1/2, p^1/3, p^1/4, etc.).

Why does this matter? While quantum field theories, such as the Standard Model, allow researchers to make predictions about particle interactions with extreme accuracy, it is still possible to improve upon current foundations of fundamental physics. When a new behavior is demonstrated—such as fractional-power scaling—scientists are given an opportunity to revisit or revise existing theories.

This work, conducted by Angelo Esposito (Institute for Advanced Study), Tomáš Brauner (University of Stavanger), and Riccardo Penco (Carnegie Mellon University), specifically considers the interactions of sound waves in solids. To visualize this concept, picture a block of wood with speakers placed on both ends. Once the speakers are powered on, two sound waves—phonons—meet each other and scatter, similar to collisions in a particle accelerator. When one speaker is adjusted to a certain limit, such that the momentum of the phonon is zero, the resulting amplitude can be proportional to a fractional power. This scaling behavior, the team explains, is not likely limited to phonons in solids, and its recognition may help the study of scattering amplitudes in many different contexts, from particle physics to cosmology.

“The detailed properties of scattering amplitudes have recently been studied with much vigor,” stated Esposito. “The goal of this broad program is to classify possible patterns of behavior of scattering amplitudes, to both make some of our computations more efficient, and more ambitiously, to build new foundations of quantum field theory.”

Feynman diagrams have long been an indispensable tool of particle physicists, yet they come with certain limitations. For example, high accuracy calculations can require tens-of-thousands of Feynman diagrams to be entered into a computer, to describe particle interactions. By gaining a better understanding of scattering amplitudes, researchers may be able to more easily pinpoint particle behavior rather than relying on the top-down approach of Feynman diagrams, thus enhancing the efficiency of calculations.

“The present work reveals a twist in the story, showing that condensed matter physics displays much richer phenomenology of scattering amplitudes than what was previously seen in fundamental, relativistic physics,” added Esposito. “The discovery of fractional-power scaling invites further work on scattering amplitudes of collective oscillations of matter, placing solids in the focus.”

About the Institute
The Institute for Advanced Study has served the world as one of the leading independent centers for theoretical research and intellectual inquiry since its establishment in 1930, advancing the frontiers of knowledge across the sciences and humanities. From the work of founding IAS faculty such as Albert Einstein and John von Neumann to that of the foremost thinkers of the present, the IAS is dedicated to enabling curiosity-driven exploration and fundamental discovery.

Each year, the Institute welcomes more than 200 of the world’s most promising post-doctoral researchers and scholars who are selected and mentored by a permanent Faculty, each of whom are preeminent leaders in their fields. Among present and past Faculty and Members there have been 35 Nobel Laureates, 44 of the 62 Fields Medalists, and 22 of the 25 Abel Prize Laureates, as well as many MacArthur Fellows and Wolf Prize winners.