Algorithms

Below I summarize various algorithms in stellar dynamics that we have developed. To obtain free copies of some of the codes, as well as software environments that facilitate running those codes, see the next page with pointers to open source codes.

Joshua Barnes and I developed a hierarchical tree code that allows calculation of interparticle forces with a scaling proportional to NlogN, as described in the article A Hierarchical O NlogN Force Calculation Algorithm, by Barnes, J. & Hut, P., 1986, Nature 324, 446-449.

Around the same time, a few other algorithms were published that scaled either either as NlogN or as N. However, the simplicity of the basic structure of our tree code was considered to outweigh whatever formal advantages the other codes may have had, given the fact that our code soon became the standard work horse of grid-free N-body simulations.

A few years later, we published a detailed analysis of the scaling of the errors in an article Error Analysis of A Tree Code, by Barnes J.E. & Hut, P., 1989, Astrophys. J. Suppl. 70, 389-417, in which we analyzed extensions of the tree code to include high-order multipole moments in the characterization of the density distribution in each cell in the tree (from quadrupole and hexadecapole up to hexacontatetrapole).

In another project, we analyzed the relative importance of the algorithmic errors in the tree code and the `real-life' errors introduced by the fact that each simulation is an arbitrary stochastic representation of an ideal density distribution, in which the particle discreteness necessarily introduces its own errors. The result were publised as Discreteness Noise versus Force Errors in N-Body Simulations, by Hernquist, L., Hut, P. & Makino, J., 1993, Astrophys. J. 402, L85-88. (Note the amusing erratum in Astrophys. J. 411, L53, in which we had to point out a superfluous `0' in the abstract, that had crept in while the paper was typeset: the first published version claimed that discreteness has intrinsic errors of 1000%....).

For a list of subsequent developments, such the analysis of Salmon and Warren who showed some interesting limitations to the choice of opening angle in simple versions of the tree code, see the literature list in Joshua Barnes' Treecode Guide.

De Kira code, developed by Jun Makino, Steve McMillan, and Piet Hut, is based on an hierarchical data structure, and uses a fourth-order Hermite integrator and an individual particle time-step scheme. It has been especially designed to facilitate interactions with order codes, such as the stellar evolution code SeBa, developed by Simon Portegies Zwart. A description of and Kira and SeBa can be found in the appendices of the article Star cluster ecology IVa: Dissection of an open star cluster - photometry, by Portegies Zwart, S.F., McMillan, S.L.W., Hut, P. & Makino, J. 2001, Mon. Not. R. astr. Soc. 321, 199-226 (also availabe as astro-ph/0005248).

The leapfrog integrator often turns out to be more accurate than you would expect from a simple second-order integrator. The `unreasonable' accuracy stems from its symmetry properties under time invariance. Intuitively speaking, a leapfrog integration of a close orbit can neither spiral in nor spiral out systematically, since such a behavior would break time reversal invariance. This marvelous property is lost, however, when we introduce variable time steps. Unfortunately, we have no choice but to adjust the time steps when we are simulating dense stellar systems, where occasionally stars come very close to each other.

To remedy this situation, we have developed an implicit algorithm in which we redefine the leapfrog for variable time steps in such a way that time reversal is maintained. In practice, the implicit scheme can often be solved in one or two iterative steps, with great gain in accuracy. The same treatment can be applied to the fourth-order generalization of the leapfrog, the Hermite scheme. Our results are described in the paper Building a Better Leapfrog, by Hut, P., Makino, J. & McMillan, S., 1995, Astrophys. J. Lett. 443, L93-L96.

Subsequent refinements were developed and published in the paper Time-Symmetrization of Kustaanheimo-Stiefel Regularization, by Funato, Y., Hut, P., McMillan, S. & Makino, J., 1996, Astron. J. 112, 1697-1708. Summaries of our techniques can be found in the conference proceeding articles Time-Symmetrized Kustaanheimo-Stiefel Regularization, by Funato, Y., Makino, J., Hut, P. & McMillan, S., 1996, in Dynamical Evolution of Star Clusters, I.A.U. Symp. 174, eds. P. Hut and J. Makino (Dordrecht: Kluwer), pp. 367-368, and Time Symmetrization Meta-Algorithms, by Hut, P., Funato, Y., Kokubo, E., Makino, J. & McMillan, S., 1997, in `Computational Astrophysics', the Proceedings of the 12th `Kingston meeting' on Theoretical Astrophysics, eds. D. A. Clarke and M. J. West, ASP Conference Series, Vol. 123 (San Francisco: ASP), pp. 26-31 (available in preprint form as astro-ph/9704276).

For the more complicated case of block time steps, there are several pitfalls that prevent a straightforward implementation. The first time symmetric treatment of block time steps was published as A New Time-Symmetric Block Time-Step Algorithm for N-Body Simulations, by Makino, J., Hut, P., Kaplan, M. & Saygin, H., J, 2006, New Astronomy xx, xxx-xxx (available in preprint form as astro-ph/0604371; in an earlier version by Kaplan, M., Saygin, H., Hut, P. & Makino, J, 2005, as astro-ph/0511304).

Significant speedup can be obtained for a wide class of N-body simulations by fine-tuning the assembly language code that is produced by N-body codes, for particular microprocessors. Speedup of a factor two can be obtained relatively easily, while in some situations speedup of up to a factor ten can be realized. See Performance Tuning of N-Body Codes on Modern Microprocessors: I. Direct Integration with a Hermite Scheme on x86_64 Architecture, by Nitadori, K., Makino, J. & Hut, P., 2006, New Astronomy xx, xxx-xxx (also available in preprint form as astro-ph/0511062).

We have developed a variety of algorithms for setting up, running, and analyzing gravitational scattering experiments. See Automatization of Scattering Experiments.

the HOP algorithm

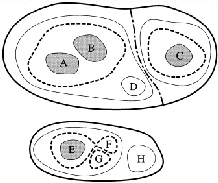In cosmological simulations of the large-scale structure of the universe, up to a billion particles are used to model the simultaneous ormation of many clusters of galaxies. To find the individual galaxies in such simulations is not easy, and it is unfeasible to carry out such searches by hand & eye - that would be too time consuming, and besides, it would introduce a human bias. Various automatic group-finding algorithms have been developed to allow computer-guided searches. In an attempt to remedy some of the short-comings of various earlier methods, Daniel Eisenstein and I developed a group-finding algorithm that is completely coordinate-free and spatially adaptive, in HOP: A New Group-Finding Algorithm for N-body Simulations, by Eisenstein, D.J. & Hut, P. 1998, Astrophys. J. 498, 137-142.

A simple way to estimate the local density in a star cluster is to divide space into a number of cells and to count the number of particles in each cell. This method is rather arbitrary and depends on the choice of grid applied. To improve this situation, Stefano Casertano and I constructed a coordinate-independent scale-free algorithm to measure local densities, based on the kth nearest neighbor distance of a particle, and we used these estimates in turn to estimate the core radii of arbitrary distributions of stars in a cluster. The algorithms were introduced and analyzed in our paper Core Radius and Density Measurements in N-body Experiments: Connections with Theoretical and Observational Definitions, by Casertano, S. & Hut, P., 1985, Astrophys. J. 298, 80-94.

Numerical Computations in Stellar Dynamics, by Hut, P., 1986, Particle Accelerators 19, 37-42.