Liquid Crystals and the Heilmann-Lieb Conjecture

Liquid crystals, discovered serendipitously by Friedrich Reinitzer in the late nineteenth century, have come to play an important role in the world of consumer electronics, specifically in the production of ever larger, thinner, and more energy-efficient displays. Starting with the small, black-and-white, monochrome displays found in many digital watches and pocket calculators, all the way to the large, colorful screens in computer monitors, flat-screen TVs, and smartphones, liquid crystals have come to form the backbone of many display technologies. As such, most of us have seen liquid crystals, used them, included them in our daily routines, let them into our homes, and allowed our children to play around with them. This beckons an important question: what is a liquid crystal?
The term itself is an oxymoron. From a materials science point of view, a crystal is characterized by order, whereas a liquid is disordered. In a crystal, the constituent atoms or molecules form ordered, regular, periodic structures, as is illustrated in figure 1a. For example, the atoms in a sodium chloride crystal (more commonly known as salt) are arranged in a simple cubic pattern, which persists over visible, human scales. This means that the atoms in a grain of salt are almost all aligned according to this simple pattern. As a striking consequence, crystals naturally take on very regular geometric shapes. In the picture in figure 1b, one can see four pyrite crystals, each of which naturally assumes the shape of a cube. This is due to its cubic molecular structure. It is rather astonishing that the tens of billions of trillions of atoms in the sample in figure 1b are all lined up!

On the other hand, the atoms or molecules in a liquid are completely disorganized, as is depicted in figure 2. In other words, there is no long-range structure, which means that the position of a molecule is independent of molecules that are sufficiently far from it, and, as a consequence, there is much more freedom in the way they are arranged. On human scales, this implies that liquids are easily deformed, and, as a consequence, flow.
Liquid crystals lie somewhere between crystals and liquids. They have order properties specific to the former, as well as disorder properties of the latter. This is made possible by the anisotropy of the shapes of the molecules in liquid crystals. While there are other examples, let us focus on compounds whose molecules are shaped like rods, that is, they are long, thin, and straight (see figure 3). Such compounds can be synthesized in the lab, and occur in nature as well: the tobacco mosaic virus, which infects tobacco plants and other nightshades, is a single strand of RNA nestled in a cylindrical shell of proteins, fifteen times longer than it is wide. In this context, a liquid crystal phase is one in which the orientations of the molecules are ordered but their positions are disordered. There are several ways in which this can occur, but let us focus on nematic liquid crystals, an example of which is depicted in figure 3a. In this phase, most of the molecules point in the same direction, up to small local fluctuations. Similar to the molecular arrangements in crystals, the molecules in a droplet of liquid crystal will nearly all point in the same direction, even though there may be billions of trillions of them. This is the ordered aspect of the configuration. On the other hand, the positions of the molecules have no long-range structure. In other words, liquid crystals flow like a liquid.

On human scales, the manifestation of this cohabitation of order and disorder properties is that, while liquid crystals flow like liquids and form droplets, the uniform orientation of its molecules gives them peculiar optical properties, that is, they interact with light in a non-trivial way. For instance, certain liquid crystals change colors as the temperature is varied. In fact, the changing colors of mood rings often come from a layer of liquid crystal under a transparent gemstone (which can be replaced by glass or plastic). Other liquid crystals change the polarization of light. Polarization is a property of light rays that is invisible to the naked eye, but plays an important role in many technological applications. Polarized light can be obtained from most common light sources (such as the sun and incandescent bulbs) by applying a simple, inexpensive filter. For example, the lenses of Polaroid sunglasses contain such filters, as do those in the glasses handed out at certain 3D movie theaters. Liquid crystals of the so-called chiral nematic type (see figure 3b) change light polarization. These liquid crystals are used to build simple electronic light filters, which are at the basis of LCD (Liquid Crystal Display) technologies.
Here, an “electronic light filter” should be understood as a device that is transparent at rest, and turns black and opaque when an electric current is run through it. Such a filter can be built by putting two polarizing filters around a chiral nematic liquid crystal. In order not to get into the physics of polarization, I will make an analogy that, while it does not capture the full depth of the theory, may be more intuitive. I will replace the light coming towards the device with a coin, and the polarizing filters with slots through which the coin must pass in order to reach the other side. The first slot is vertical, while the second is horizontal. The coin is initially vertical, but the chiral nematic liquid crystal rotates it by 90 degrees as it passes through it. Thus, the coin goes through the vertical slot and is rotated by the liquid crystal so that it can pass through the horizontal slot to the other side. Beyond the analogy, this means that light can go through the filter, which is, thereby, transparent. If an electrical current is run near the liquid crystal, it turns the chiral nematic phase (figure 3b) into a regular nematic phase (figure 3a), which does not change the polarization of light, and, in the analogy, does not rotate the coin. Thus, when a current is run through the device, the coin is still vertical when it reaches the horizontal slot and cannot fit through. Light cannot go through the filter, which turns black and opaque.
In digital watch displays, each digit is assigned seven rod-shaped electronic light filters. In order to display a number, the appropriate filters are switched on, which turns them black. The mechanism used in computer monitors, TVs, and smartphones is slightly different, but conceptually similar. Images are broken up into several million colored dots, called pixels. Each one is a red, green, or blue light source with an electronic light filter in front of it. By turning the appropriate filters on or off, the intensity of each pixel is adjusted, and an image is displayed.
Let us briefly summarize what we have so far: liquid crystals are materials that exhibit order in the orientations of their molecules, and disorder in their positions. They flow like liquids, and interact with light in intriguing and useful ways. From a scientific point of view, the natural next question is: how do liquid crystals exist? Put another way, can one find a model that adequately represents the molecules in a liquid crystal, in which one can prove that the molecules spontaneously align, and yet flow?
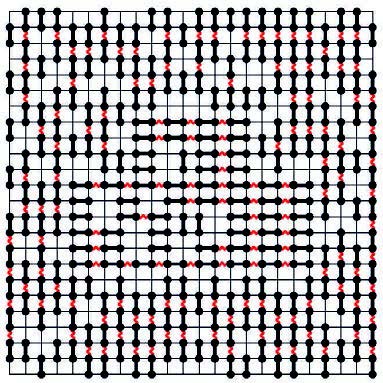
A partial answer was provided in the pioneering work of Lars Onsager in 1949, in which it was shown that, under certain approximations, systems of many long rods spontaneously form nematic liquid crystals. But without such approximations, little was known until 1979, when Ole Heilmann, a chemist from Copenhagen, and Elliott H. Lieb, a mathematical physicist from Princeton University, introduced a family of models which may have a provable liquid crystal phase. I will now describe one of these, which I will call the Heilmann-Lieb model. First of all, it is a two-dimensional model, that is, it describes a liquid crystal on a flat surface. Second, it is defined on a grid, so the molecules are restricted to a square mesh. The molecules are represented as length-1 rods on this grid, as shown in figure 4. They can only take one of two orientations: horizontal or vertical. In addition, we introduce forces between the rods which favor alignment. One can think of these interacting rods as magnetized sticks, which tend to align with their neighbors. Heilmann and Lieb proved that the rods spontaneously align in this model. Therefore, there is order in the orientation of the molecules. They did not prove that their positions are disordered, but conjectured it should be so. I will call this the Heilmann-Lieb conjecture.
Since the Heilmann-Lieb conjecture was formulated, other models were introduced in which the existence of nematic liquid crystal phases was proved. In the fall of 2016, Elliott H. Lieb, who had formulated the conjecture in 1979, and I revisited the Heilmann-Lieb model, and have recently announced a proof of the conjecture. Thus, in the Heilmann-Lieb model (in the appropriate range of parameters), the molecules spontaneously align, and yet, they flow, which implies that the system behaves like a nematic liquid crystal.
But one important open question remains. In the Heilmann-Lieb model, the molecules can only take two orientations, whereas in a real liquid crystal, they can point in any direction. Can one find a realistic molecular model, in which the orientation of the molecules is unrestricted, for which a liquid crystal phase can be proved to exist? By improving our understanding of simplified models, such as those introduced by Heilmann and Lieb, we are inching closer to the answer.


