Using Protein Sequences to Predict Structure

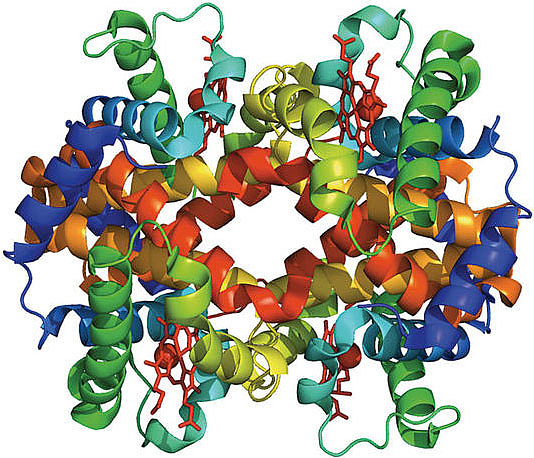
Proteins are typically cited as the molecules that enable life; the word protein stems from the Greek proteois meaning “primary,” “in the lead,” or “standing in front.” Living systems are made up of a vast array of different proteins. There are around 50,000 different proteins encoded in the human genome, and in a single cell there may be as many as 20,000,000 copies of a single protein.¹

Each protein provides a fas­cinating example of a self-organ­izing system. The molecule is assembled as a chain of amino acid building blocks, which are bonded together by peptide bonds to form a linear polymer. Once synthesized, this polymer spontaneously self-assembles into the correct and highly ordered three-dimensional structure required for function. This ability to self-assemble is remarkable—each linear polypeptide chain is highly disorganized, and has the potential to adopt an array of conformations so vast that we cannot enumerate them, yet within less than a second a typical protein spontaneously assumes the correct, highly ordered three-dimensional structure required for function. The identity and order of the amino acids that make up this polypeptide, that is the protein sequence, typically contain all the information necessary to specify the folded functional molecule.²

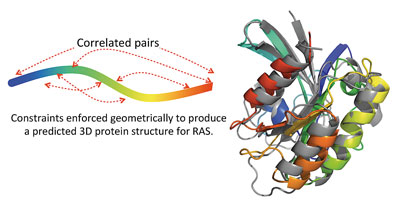
Figure 1: A) The amino acids (letters, second row of table) specified at each sequence position (numbered, top row of table) for a particular protein are synthesized into a polypeptide chain. B) The polymer chain spontaneously self-assembles into the complex three-dimensional structure specific to that protein that is required for the molecular function. C) Once folded, the protein is described as a monomer, and often different monomers or multiple copies of the same monomer self-assemble into protein complexes that form functional molecules.

We currently live in a hugely exciting time for the biological sciences, for the simple reason that technological advances have greatly increased our ability to accurately collect large amounts of data. In particular, over the last twenty years our ability to cheaply and precisely determine the sequences of proteins has vastly increased, leading to the assembly of large, freely accessible collections of protein sequences from different species. However, experimentally determining the three-dimensional structure of a protein is expensive and difficult, leading us to ask if we can use the sequence data available for each protein to predict its three-dimensional structure. The crucial point is that the sequence of a particular protein varies between different species. Hemoglobin (figure 1), the protein in our blood that binds and transports oxygen, provides a good example. Versions of hemoglobin from different species are very similar, both in their three-dimensional structure and in the function they carry out. How­ever, there are differences between the hemoglobin amino acid sequences that occur in different species. An exciting current direction of research is to exploit this evolutionary sequence variation and crack the code that relates amino acid sequence to protein structure and function.^3,4

Model based on sequence data
The basic idea is to use the abundance of protein sequence data that is now available to build a probability model for the amino acid sequence that codes for each protein of interest. The probability distribution for the sequence, P(A1, A2, ..., An), describes the probability that each of the twenty amino acids occurs at each of the positions 1,...,n in the sequence of n amino acids that makes up the protein of interest. If we are able to collect enough distinct data samples for a protein of interest, and we make certain assumptions about the mathematical form of the probability distribution, then we can use the data to infer the parameters of the model. For many proteins, upwards of 10,000 sequences are now available, a body of data that constitutes a set of samples from this probability distribution, though the elements of this set are not sampled independently of one another.

What form should the probability model take? The space of models that would generate the data observed for a particular protein is unbounded. However, we can use the knowledge about proteins collected by biologists over the last century to restrict our attention to particular classes of models. A process of selection on standing variation in different populations produces sequences of a particular protein across many species. Through the evolutionary process, mutations (amino acid changes) at different sequence positions within a protein are randomly generated. Some of these mutations lead to an improved version of the protein, increasing the fitness of the organism, and will therefore be selected. There is a high-dimensional space of possible sequences; the sequences corresponding to a protein of interest occupy some subset of this space. Sequences collected in the database that code for a particular protein record the outcomes of millions of evolutionary experiments that probe the boundaries of this subset. The boundaries are imposed by the requirement for a protein to be functional; the idea is to infer the boundaries, or constraints, on which sequences are allowed, and thus learn about the relationship between amino acid sequence and protein function.

A key point is that mutations at different sites do not necessarily have independent effects on the protein. In particular, it is often observed that while a single mutation at one position within a sequence results in a protein that is no longer functional, perhaps because it does not fold correctly, this disability can be rescued by a compensatory mutation that occurs elsewhere in the protein sequence. This suggests that we need to include interactions between different sequence positions in the probability model. Though the number of sequences available for many proteins is large, the space of possible parameters for a model that considers interactions of different orders is much larger, and so we restrict our attention to models that consider pairwise interactions between different sequence positions. We hypothesize that if two amino acids are in close proximity in the three-dimensional protein structure​—if they pack against each other, for example, or interact via a hydrogen bond—then their mutation pattern across different species may contain correlations, as in the toy model illustrated in figure 2. If this model is accurate, it suggests that it may be possible to use pairwise interactions to predict the spatial proximity of amino acids in the three-dimensional protein structure from sequence data.

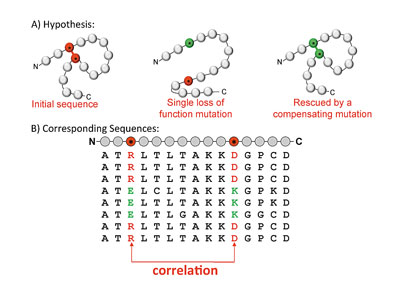
Figure 2: A) The toy model illustrates an example where a mutation at one sequence position results in a protein that no longer folds or functions correctly. This loss of protein function is rescued by a compensatory mutation elsewhere in the sequence, restoring the ability of the molecule to fold and function. B) If this model is correct, it will mean that our sequence database only contains sequences with i) neither of the mutations, or with ii) both of the mutations, and hence the mutation pattern of the two columns that correspond to these two sequence positions will be correlated.

Experimentally determining the three-dimensional structure of a protein of interest is an expensive and time-consuming process, and for many transmembrane proteins (insoluble because they span the hydrophobic lipid bilayer that bounds a cell), it is not yet possible. The question of predicting the three-dimensional structure of a protein from its amino acid sequence has occupied scientists for at least the last fifty years. Part of the reason that this problem is rather intractable is the sheer number of possible conformations that each protein chain could in theory adopt. Each protein chain typically contains hundreds or in some cases thousands of amino acids.

To compute a rough estimate of the order of magnitude of the conformational search space, consider that each amino acid has two independent bond angles that describe its conformation within the context of a polypeptide chain, and add to this at least one extra degree of freedom describing the orientation of the amino acid’s side chain. Assuming, conservatively, that each degree of freedom can only take a restricted set of say 10 values, this provides a minimum of 10³=1000 different structural conformations per amino acid—that is (10³)¹⁵⁰ possible configurations for a protein consisting of just 150 amino acids. Even if there is flexibility in the native structure—if amino acid side chains are able to rotate to some extent, for example—the native folded structure of a protein occupies just a tiny fraction of this enormous space, making it computationally intrac­table for any sort of brute force search approach. If the chain were able to sample conformations at a nanosecond or picosecond rate, it would still take a time longer than the age of the universe to find the correct native conformation (Levinthal’s paradox).⁵ The fact that proteins manage to fold on biologically relevant timescales suggests that protein sequences are optimized by the evolutionary process to enable fast and reliable folding.

The shape of the energy landscape that enables the protein to spontaneously self-assemble into the correct structure in a matter of seconds is dictated by the physical interactions between different amino acids. Attempts have been made to use approximations of the physical interactions both between atoms of the protein and with atoms of the surrounding solvent to computationally simulate the protein-folding problem. While progress has been made, allowing the structures of some small proteins to be accurately predicted, the problem remains computationally intractable even with the use of coarse-grained approximations. Currently, we are unable to simulate more than a millisecond of protein dynamics, which prevents the simulation of folding trajectories for larger proteins.

The probability model
The question is how we can best use the available sequence data to infer the constraints or bounds on the space of amino acid sequences that result in the particular protein of interest. This is a typical inverse problem; we wish to use the data to infer the model constraints, i.e., to parameterize the probability distribution. This raises the crucial question of what form the probability distribution should have. While we require that the probability model reproduce the statistics of the observed data, there are many models that will do this. We wish to choose a single model from among these, so we choose the maximum entropy model, i.e., the least constrained model that reproduces the observed data. Specifically, we ask for the single site marginals and the marginals for each pair of sites to match the empirical frequency counts for the single sites, and each pairs of sites, in the sequence alignment available for the protein of interest. The resulting Potts model, known from statistical physics, defines a global probability model on the space of protein sequences: Where e_ij(a,b) are called the couplings, and h_i the fields.

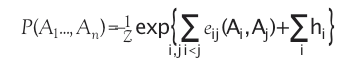
Here 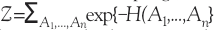is the partition function, which ensures that the probabilities are properly normalized.

A different model is built from data for each protein, and gives the probability that any sequence of interest will specify the protein for which the model is built. In short, the set of sequences available for a protein of interest is used to infer the parameters for this model.

One prediction is that those pairs of sequence positions that have the highest interaction score will be in close structural proximity in the three-dimensional protein structure. To test the predictive power of our inference procedure, we compare the highest scoring pairs of sequence positions to the experimentally solved crystal structure of an example protein. In figure 3, the match between the model predictions (red stars) and the crystal structure data (grey points) is shown to be excellent.

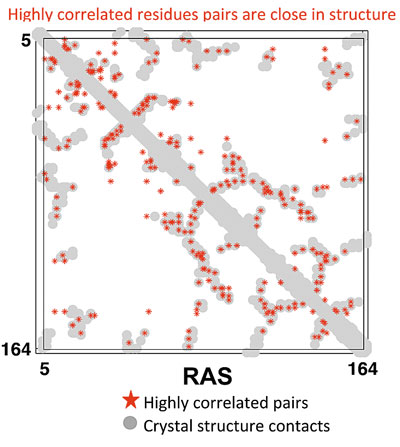
Figure 3: In grey is a two-dimensional map of the three-dimensional crystal structure data—this is a binary matrix where a ‘1’ represents two amino acids between which the distance in the crystal structure is less than 5 angstroms. The highest scoring amino acid pairs from the maximum entropy model inferred from sequence data are plotted in red. The fact that many of the red points coincide with grey points demonstrates that we can predict information about three-dimensional protein structure from sequence data.

This is a highly surprising result, which immediately raises the question of whether the information inferred from sequence data is sufficient to predict the three-dimensional protein structure. To test this hypothesis, we start with the unfolded polypeptide chain for the protein of interest, and use an algorithm called distance geometry to enforce that the two amino acids in each high-scoring pair are within 7 angstroms of each other in our structural model. Distance constraints that reflect the secondary structure predicted from protein sequence are also included.

Figure 4: Comparison of our predicted three-dimensional protein structure for the protein RAS with the crystal structure (grey). The root mean square deviation between the C∝-atoms of our predicted structure and the experimentally solved crystal structure is 3.5 angstroms, comparable to a low-resolution crystal structure.

We find that there is indeed sufficient information in these large sequence alignments to accurately predict protein three-dimensional structure.⁶ This statistical method makes progress on the protein-folding problem by predicting, from sets of protein sequences, structures for a range of globular and transmembrane proteins. In addition, three-dimensional structures were predicted using these methods for a set of transmembrane proteins for which no experimental structure had yet been solved. Many of these
proteins are important in human diseases, and the existence of predicted structures will allow models of their function to be constructed and potentially validated. While the ability to use evolutionary variation to shed light on protein structure is exciting, the fundamental question of the relationship between amino acid sequence and protein function requires further work. In particular, it will be important to understand how the concerted actions of groups of amino acids within a protein result in different protein phenotypes, and fur­ther­more how these can be predicted from large collections of protein sequences.^3,4