Extrasolar Planets and the New Astronomy
The desire to discover distant, rare, and strange objects dominated twentieth-century astronomy, for which increasingly larger and more sensitive telescopes were constructed.
The act of carrying out this objective has brought enormous—and somewhat unbelievable—rewards: We now accept that we orbit a thermonuclear furnace, the Sun, whose physical properties are quite common, so common that there are nearly 100 billion Sun-like stars within our galaxy, the Milky Way. It was discovered that the Milky Way was not, in fact, the entire Universe; the observable Universe is of order many billions of light years across (that’s big), and there are of order 100 billion galaxies like our own floating around within it. In the center of these galaxies there happen to be super-massive black holes whose masses can be up to 10 billion times the mass of the Sun. When these enormous black holes are built up by in-falling gas, they are called “quasars,” and produce the equivalent of 100 trillion Suns worth of light within a volume comparable to our solar system. The greater the separation between any two galaxies or quasars, the greater the rate at which they move apart or, in other words, the Universe is expanding. Perhaps even more surprising, the Universe is primarily made up of stuff that we can neither see nor feel, i.e., dark energy and dark matter. The strategy of building bigger and more sensitive telescopes, meanwhile, has produced a growing number of “smaller” results that continue to employ regiments of astronomers: gamma-ray bursts, pulsars, X-ray emitting binary stars, clusters of galaxies, cosmic microwave background radiation, and the list goes on.
The general pursuit of the twentieth century continues with the planned construction of the billion-dollar-plus U.S.-led Giant Magellan and Thirty-Meter Telescopes, as well as the European Extremely Large Telescope. However, a new strategy for discovery has emerged in the twenty-first century: time-domain astronomy. Rather than finding faint and distant sources, searching in the time-domain enables the discovery, for instance, of small variations of relatively bright nearby objects, such as stars. An exciting source of such small brightness variations are extrasolar planets or, in other words, planets that orbit around other stars.
The basic approach of time-domain astronomy is easy enough to state. Look somewhere in the sky and then look at it again, some time later. If anything has changed, study it further. The time it takes for the instrument to reobserve the same patch of sky is referred to as the “cadence.” By using the old strategy of looking deep and far into the Universe, sources of a given brightness are methodically mapped out in a three-dimensional volume. In time-domain astronomy, sources that vary by some brightness with a rate equal to the inverse of the instrument cadence can be steadily mapped out. In a way, the time-domain adds another dimension, given by the frequency equal to the inverse cadence, to the properties of observed phenomena.
Interestingly, one can either go deep with a relatively big telescope, coming back to the same field of view every once in a while, or one can go shallow with a relatively small telescope and a short cadence. Since we don’t know what’s out there, each approach seems equally valid.
An important point to keep in mind: small telescopes typically have relatively large fields of view in comparison to big telescopes. Since small telescopes are much cheaper to construct than big telescopes, the cost of mapping out the Universe in the time-domain may be done more efficiently with smaller instruments that have rapid cadence. Perhaps the next century of astronomical discovery will be dominated by several small groups of enterprising individuals, armed with batteries of modest telescopes, competing with one another to map out the time-domain. For years, such a view of astronomy’s future was enthusiastically advocated by the late Bohdan Paczynski of Princeton University (a frequent Visitor in the School of Natural Sciences between 1974–81), who initiated two successful time-domain campaigns: the All-Sky Automated Survey and the Optical Gravitational Lensing Experiment.
Paczynski realized early on that the only way to achieve this was to take full advantage of astronomy’s impending digitization. Modern telescopes equipped with CCD cameras (like the one in your cell phone), rather than the old photographic plates, produce pixel-by-pixel electronic images of the sky that can be stored and manipulated by a computer. Only with the help of massive amounts of custom-built software and fast processors would it be possible to explore massive volumes of the Universe in the time-domain with great precision.
Consider repeatedly scanning a huge number of Sun-like stars in the Milky Way with high cadence at great precision, in order to look for small differences in their emitted light. As previously mentioned, an interesting source of such small differences may be a planet that orbits around its host star, i.e., an extrasolar planet. In the case where a planet passes in front of its host, a small (about 1 percent for a big planet) momentary depression in its brightness, or an eclipse, can be observed. Such an eclipse is usually referred to as a “transit” and is one of the most successful methods of detecting extrasolar planets. Today, we know the properties of approximately 1,000 extrasolar planets. Twenty years ago, at the beginning of the digital age, that number was zero. Paczynksi was right.
The primary motivation for studying extrasolar planets is to find another place in the Universe that closely resembles our own planet, i.e., another Earth. Since an Earth-sized planet is quite small in both size and mass in comparison to its stellar host, its ability to deform the appearance of its host is correspondingly limited. Its transit in front of a Sun-like star would lead to a depression in brightness that is of order 1 percent of 1 percent. Only now are instruments sensitive enough to detect an Earth analogue. If they are out there in significant number, the recently launched Kepler space observatory, a high-precision extrasolar-planet-transit-detecting-machine, should report on their discovery any day now.
|
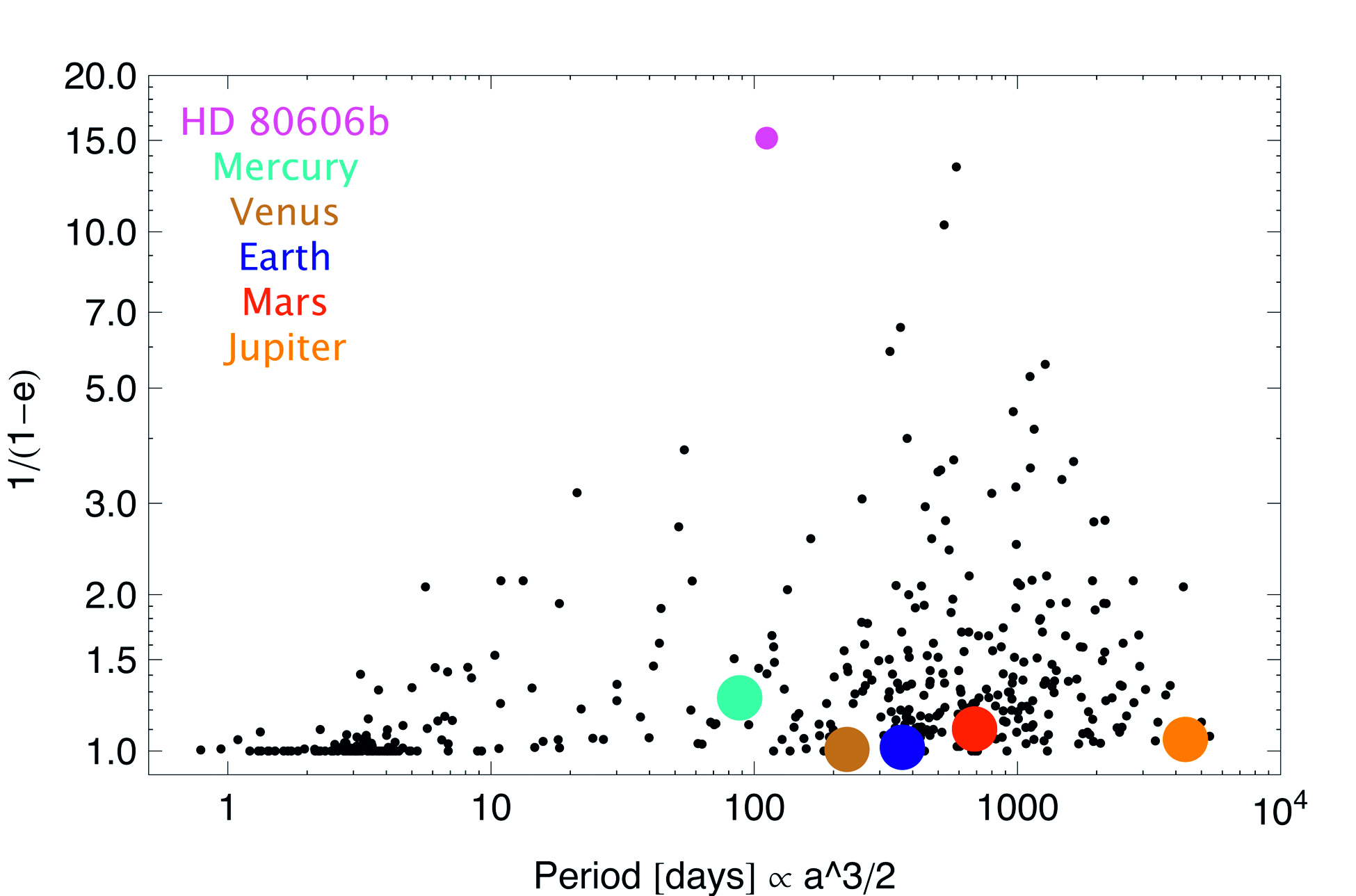
| Figure 1: A measure of eccentricity e versus orbital period for gas giant extrasolar planets, i.e., planets like our Jupiter and Saturn. The inner five planets of our solar system are included as well. In general, the physical processes that lead to planet formation produce solar systems that are unlike our own. The overwhelming majority of the planets depicted in this graph orbit Sun-like stars. (Data: www.exoplanets.org) |
But, what about the 1,000 or so extrasolar planets whose properties (mass, radius, orbit, etc.) we know of? Figure 1 clearly shows that other solar systems are commonly quite unlike our own.
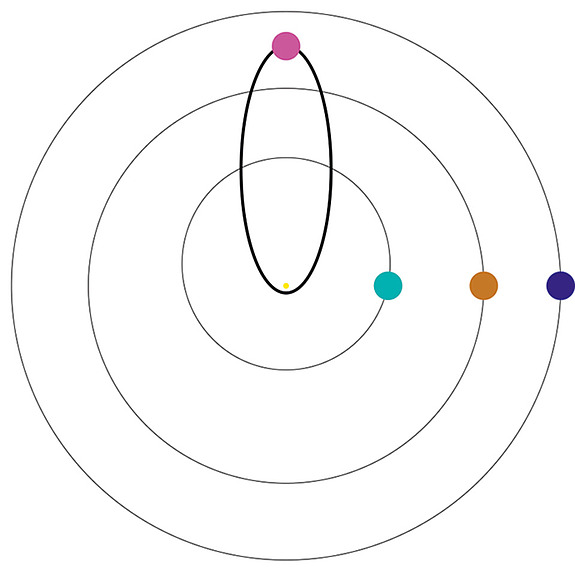
The shape of a planet’s orbit is well approximated by an ellipse where the stellar host resides at one of the focus points. In the limit that the ellipse is a perfect circle, the eccentricity e is equal to zero, and in the other extreme, where the orbit is a parabola, e is equal to one. Figure 1 tells us that, unlike our solar system, the eccentricity of big planets, like our Jupiter, can take on almost any value. Note the magenta point in Figure 1, which depicts HD 80606b, the most eccentric planet known to date, with e=0.93! Figure 2 (at top) depicts what its orbit would look like if it were placed in our solar system.
It is generally presumed that gas giants are formed at large separation from their host stars. Therefore, the cluster of gas giant planets with short orbital periods, known as the “hot Jupiters,” in Figure 1 came as quite a surprise. In order to account for their close-in orbits, the concept of “migration” is often invoked, meaning the planet was formed far away from its stellar host and then some mechanism removed its orbital energy such that its average heliocentric distance was reduced by a factor of 100 or more. Such a notion seems unbelievable, but the fact that the hot Jupiters exist in relatively large numbers (about 1 percent of all Sun-like stars have one) forces us to seriously consider it.
A popular class of hot Jupiter migration scenarios involves the introduction of a third body, such as another giant planet or a stellar companion (about half of all stars are in binaries). The gravitational interaction between the third body and a gas giant can exchange orbital angular momentum, but roughly conserves orbital energy. In the event that most of the angular momentum is extracted from the gas giant’s orbit, the eccentricity becomes large and the distance of closest approach, called “periastron,” becomes very small, much like HD 80606b.
As the planet comes toward periastron, the tides raised on the planet rapidly increase in strength. In fact, the height of the tide increases with the inverse of distance, cubed. The energy stored in the tidal flow increases with the inverse of distance to the sixth power. Tidal friction during closest approach then allows energy to be drained from the orbit and converted into some form of heat within the planet, which is then radiated into outer space. Consequently, the average heliocentric distance slowly shrinks as a result of tidal friction such that a gas giant with an initial period of several years ends up in a circular orbit with a final period of a few days where migration ends (see Figure 3). Such a process within a solar system seems unbelievable, but again, the observations require that we seriously consider it.
|
| Figure 3: Depiction of high-e migration of HD 80606b (magenta). The outer ellipse corresponds to a planet with HD 80606b’s orbital angular momentum, but with an orbital period of twelve years, equal to that of our Jupiter. The sequence of ellipses of diminishing eccentricity illustrates how tidal dissipation at closest approach to the stellar host slowly removes orbital energy, shrinking the orbit, but conserving angular momentum. At the end of its migration, HD 80606b’s orbit will be the small circular orbit, with a final period equal to 5 days. For reference, the orbits of the inner three planets of our solar system are shown. |
IAS Members Subo Dong and Boaz Katz, Professor Scott Tremaine, and I have proposed a simple test of this “high-e” migration scenario. Our arguments begin with a rather unsophisticated fact: stars in the Milky Way are formed roughly in a steady state shortly after the birth of the Universe. Since planet formation is a byproduct of star formation, planets are therefore formed in a steady state as well. So, if we see some number of gas giant planets with moderate eccentricities that may end up becoming short-period hot Jupiters, we should see many super-eccentric gas giants on their way in. In fact, for every HD 80606b, there should be several gas giant planets with record-breaking eccentricities. One reason why these super-eccentric Jupiters have not been detected so far may be due to previous limitations in detector sensitivity and observational strategy. Interestingly, the Kepler space observatory does not suffer from such deficiencies, and we predict that it should detect anywhere from a handful to a dozen super-eccentric gas giant planets if high-e migration is at work.
In the last century, bigger and bigger telescopes were built largely to find sources of light that are far away and strange. On the way to discovering rare beasts, like quasars, we realized that we orbit a rather common star, which itself orbits within a rather common galaxy, and the Universe contains billions of each. By mapping out the vast wilderness that is the Universe, the notion that we are quite ordinary was unexpectedly reinforced.
By examining close-by stars similar to our Sun with great precision in the time-domain, the basic expectation was to find solar systems that are like our own. We now realize that the architecture of our solar system is not typical—it is only one of a vast variety of possibilities. In our attempts to confirm that there are places in the Universe like our own, we have found that the particular place we occupy is, in some ways, rather strange.
Is there any meaning to all of this? Probably. But, I am running out of space and expertise. What I can say for sure is that the Universe has a tendency to disregard our expectations. Maybe there is a lesson in that.
For more information, see http://arxiv.org/abs/1110.1644.