Open Problems in Mathematics with John Nash

“This therefore, is mathematics: she reminds you of the invisible forms of the soul; she gives light to her own discoveries; she awakens the mind and purifies the intellect; she brings light to our intrinsic ideas; she abolishes oblivion and ignorance which are ours by birth.”——Proclus

Looking back in life, there are experiences that one considers important and stand out, whereas others just become memories that fade away. However, sometimes, experiences might be so precious or even surreal that it takes time to digest that they were even part of your past in the first place. Such experiences might even influence aspects of your life altogether. Spending time and collaborating with John F. Nash, Jr., was one such experience.

It all started in September 2014, in one of the afternoon coffee/tea meetings that take place on a daily basis in the common room of Fine Hall, the building housing the Mathematics Department of Princeton University. John Nash silently entered the room, poured himself a cup of decaf coffee, and then sat alone in a chair close by. That was when I first approached him and had a really pleasant chat about problems in the interplay of game theory and number theory. From that day onwards, our discussions became ever more frequent. From the common room to his office, to the library and the beautiful parks of Princeton, our discussions about various topics in mathematics often led us—in one way or another—to some intriguing open problem in mathematics. In one of those occasions, we happened to chat about David Hilbert’s famous list of twenty-three problems. That very mathematical/philosophical dialogue influenced our later decision to collaborate on the preparation of a book titled Open Problems in Mathematics, recently published by Springer. Of course, as we also explain in the preface of our book, we intended neither to compare (in any degree!) nor to associate our list of open problems with that of the great Hilbert. After all, this would be almost blasphemy. Among the readers of the present article, mathematicians surely know and non-mathematicians probably don’t know about Hilbert’s list. Thus, I now briefly write for the latter readers a few words to clarify this mysterious list of twenty-three problems and how it came about.

More Math Mysteries Book Marks Last Chapter for ‘A Beautiful Mind’ Whiz John Nash By Kelly Heyboer, NJ.com
Every four years in one city of the world, the International Mathematical Union hosts the International Congress of Mathematicians (ICM), which is the largest and most prestigious conference devoted to the field of mathematics. The first (official) ICM was held in Zürich in 1897. There were just a few exceptions when the ICM was not organized after a period of four years. The first such exception¹ was 1900, when the second ICM took place in Paris. This happened so that it would coincide with the Exposition Universelle in Paris and, most importantly, so that this ICM would mark the opening of the new century of mathematics. A couple of years prior to this event,² the great French mathematician Henri Poincaré proposed to Hilbert the preparation of a list as well as an elaborate presentation of open problems that Hilbert considered to be the most—or among the most—important open problems in the entire field of mathematics at that time: a list of open problems that would help guide generations of bright mathematicians for the coming century. Hilbert accepted Poincaré’s proposition, and for the ICM of 1900 he prepared his celebrated list of twenty-three problems.³ This collection of open problems has been extremely influential and has channeled a great deal of important research ever since. Several prominent figures in the history of mathematics from 1900 onward invested years of research in their efforts to solve one of Hilbert’s problems. One of those luminaries was Nash, who independently of Ennio de Giorgi solved Hilbert’s nineteenth problem. At the time of my discussion with Nash in September 2014 about Hilbert’s problems, we decided to prepare together the book Open Problems in Mathematics. The content of that dialogue can be mainly summarized by the following part of the preface we later jointly composed for our book:

It has become clear to the modern working mathematician that no single researcher, regardless of his knowledge, experience, and talent, is capable anymore of overviewing the major open problems and trends of Mathematics in its entirety. The breadth and diversity of Mathematics during the last century has witnessed an unprecedented expansion. […] Perhaps Hilbert was among the last great mathematicians who could talk about Mathematics as a whole, presenting problems which covered most of its range at the time. One can claim this, not because there will be no other mathematicians of Hilbert’s caliber, but because life is probably too short for one to have the opportunity to expose himself to the allness of the realm of modern Mathematics. Melancholic as this thought may sound, it simultaneously creates the necessity and aspiration for intense collaboration between researchers of different disciplines. Thus, overviewing open problems in Mathematics has nowadays become a task which can only be accomplished by collective efforts.

The above excerpt basically manifests the ideology with which this project was initiated. The day we made the decision to prepare this book, Nash turned to me and said with his gentle voice, “I don’t want to be just a name on the cover though. I want to be really involved.” After that, we met almost daily and discussed mathematics for several hours at a time, examining a vast number of open problems ranging over several areas. During these discussions it became even clearer to me that his way of thinking was very different from that of almost all other mathematicians I have ever met. He was thinking in an unconventional, most creative way. His quick and distinctive mind was still shining bright in his late eighties. He still had this spark, the soul of a young mathematician. The fact that he moved slowly and talked with a quiet voice had nothing to do with the enthusiasm with which he did mathematics. The scope of the book we were preparing was to publish invited survey papers by world experts presenting the status of some essential open problems in pure and applied mathematics, including old and new results as well as methods and techniques used toward their solutions. One expository paper is devoted to each problem or constellation of related problems.

After having been asked to contribute the present article regarding the experience of working with John Nash, I started recollecting all those moments from my privileged year as his collaborator and frequent companion. Among all those memories, I recalled a freezing winter day at Princeton that still makes me shiver. It was late January 2015, classes and seminars were canceled, and the University had advised all its members to remain home due to an upcoming snowstorm. Nash and I also postponed our meeting until the storm would pass. While working from home that night, I received from him an email, which was a kind of an account or even a testimony of his career as a problem-solver. Interestingly enough, he didn’t mention his work in game theory for which he is more widely known. It also surprised me that he signed the email with his full name rather than just “John” as he would normally do in our correspondence. This email is enclosed below.

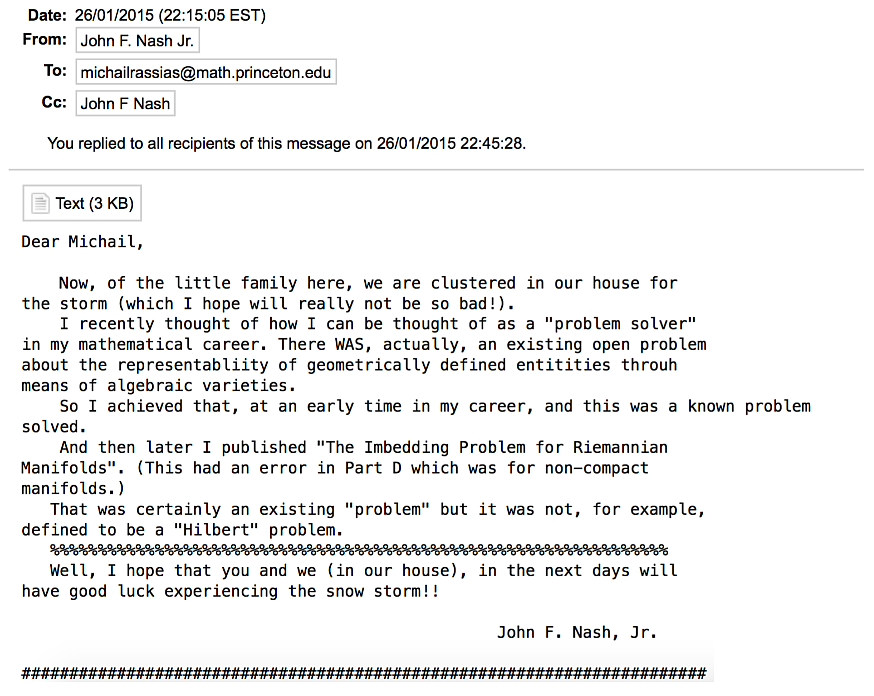
Months went by, winter passed, and our almost daily discussions continued and remained deeply interesting, as well as a source of everlasting inspiration for me. The book was nearly ready before John and Alicia Nash left in May for Oslo, where he was awarded the 2015 Abel Prize from the Norwegian Academy of Science and Letters. We had even prepared the preface of this volume, which he was so much looking forward to seeing published.

On this occasion, I would also like to say just a few words about the man behind the mathematician. In the famous movie A Beautiful Mind, which portrayed his life, he was presented as a really combative person. It is true that in his early years he might have been, having also to battle with the demons of his illness. Being almost sixty years younger than he, I had the chance to get acquainted with his personality in his senior years. All the people who were around him, including myself, can avow that he was a truly wonderful person. Very kind and disarmingly simple, as well as modest. This is the reason why, among friends at Princeton, I used to humorously say that the movie should have been called A Beautiful Mind and a Beautiful Person. What was certainly true, though, was the dear love between John and Alicia, who together faced and overcame the tremendous challenges of John Nash’s life. It is somehow a romantic tragedy that fate bound them to leave this life together on their return from Oslo, where Nash had received the Abel Prize, in May 2015.

One can say that among the mathematicians who have reached greatness, there are some—a selected few—who have gone beyond greatness to become legends. John Nash is one such legend. I remember when there was a celebration organized at the Mathematics Department of Princeton University in March 2015 for the announcement that Nash and Louis Nirenberg would share the 2015 Abel Prize, Morgan Kelly from the University’s office of communications asked me what was it like to collaborate with John Nash. What I felt then about my collaboration with Nash is what I still feel now. If you were a musician and had an opportunity to work with Beethoven and compose music with him, it would be astonishing. This was the same thing. If a mathematician of the stature of John Nash so generously invests his time and energy in a researcher more than half-a-century younger, it makes you wonder what we should do, when the time comes, for the younger generations of scientists eager to learn and explore.