In the beginning of the twentieth century, the University of Göttingen was one of the top research centers for mathematics in the world. The mathematician David Hilbert was a well-established professor there, and during the winter semester of 1924–25 he gave a series of lectures about the infinite in mathematics, physics, and astronomy. (These and other lectures by Hilbert are now published in book form by Springer-Verlag. The book is available at the IAS library in translation and in the original German.) In one of these lectures, he used an example to explain the crucial difference between finite and infinite sets: in a hotel with a finite number of rooms, if all rooms are occupied then there is no room for new guests. But in a hotel with infinitely many rooms this is not a problem: if all rooms are occupied and a new guest arrives, simply move each old guest one room over, leaving the first room vacant for the newly arrived guest. A similar argument lets us accommodate any finite number of, and even infinitely many, newly arrived guests.
George Gamow (of the famously authored Alpher–Bethe–Gamow paper in the field of physical cosmology) was a summer postdoc at the University of Göttingen a few years after these lectures happened and probably learned of Hilbert’s example of the infinite hotel there. He popularized it in his 1947 popular science book titled One Two Three...Infinity: Facts and Speculations of Science (available at the Princeton University library).
Let us get back to Hilbert’s hotel. To make things neat, let us say that the hotel’s infinitely many rooms are numbered 1, 2, 3, 4, 5, . . . . One night, they are all occupied but a new guest arrives. As we said before, we simply move the guest in room 1 over to room 2, the one in room 2 over to room 3, the one in room 3 over to room 4, and in general, the guest in room n over to room n + 1, thereby creating a vacancy in room 1 for the new guest, but leaving none of the original guests homeless.
Now say twenty new guests arrive rather than just one. The trick used before works just as well: move the guest in room 1 to room 21, the guest in room 2 to room 22, and in general, the guest in room n to room n + 20. This will leave twenty rooms vacant and ready for the twenty new guests.
But what if infinitely many new guests arrive aboard an infinite bus? We can modify the previous argument so that it still works for this situation: space out the guests already in the hotel so that they only occupy every other room. Mathematically speaking, move the guest in room n to room 2n, so that all the even-numbered rooms are occupied. This leaves every other room (infinitely many!) vacant and ready to accommodate the (infinitely many!) people arriving by the bus. The person sitting in seat number n on the bus should move into the nth odd numbered room, which is room number 2n − 1.
What if ninety-nine infinite buses arrive? Simply move the original hotel guests to rooms 100, 200, 300, etc., the passengers of the first bus to rooms 1, 101, 201, etc., the passengers on the second bus to rooms 2, 102, 202, etc., and so on for the rest of the buses. This will occupy all rooms of the hotel while leaving no guests without a room. If the passengers on the buses were themselves numbered 1, 2, 3, 4, 5, . . . (and let us make no distinction and call the original guests of the hotel passengers as well—we can think of it as moving all the original guests out of the hotel and into a decorative bus parked right outside the hotel, which we can call bus number 0), then we would see the first one hundred rooms of the hotel are filled with passengers number 1, the second hundred rooms of the hotel are filled with passengers number 2, and so on.
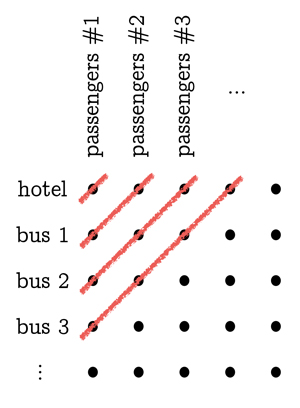
The next level is dealing with infinitely many infinite buses (each bus with infinitely many passengers). The first thing to do is to get everyone out of the hotel and out of the buses and organized in grid like form in the parking lot, or on a piece of paper: have the original guests of the hotel (a.k.a., passengers of bus 0) line up in order, left to right, forming a row. Have the passengers from the first bus form another row just below it, and the passengers from the second bus a row below that one, etc. Make the rows line up with each other so that passengers number 1 from each bus line up in a column, passengers number 2 line up in a column to the right of that one, and so on. Now, if we start filling up hotel rooms 1, 2, 3, 4, . . . with people from the first row, we will never finish it and move on to the second row, and similarly if we try to start with the first column. The trick is to think of diagonal lines, running bottom-left to top-right on the grid. The leftmost of these diagonal lines only hits the one top-left person (bus 0, passenger 1): put that person in room 1. The next diagonal line hits two people (bus 1, passenger 1 and bus 0, passenger 2): put those two people in rooms 2 and 3. The next diagonal line hits three people: put them in the next three empty rooms, 4, 5, 6. Continuing this pattern we will eventually assign a room to each of the people patiently standing in the parking lot.
Can we go deeper into infinity, deeper than infinitely many infinite buses? Yes we can: imagine that right next to Hilbert’s hotel is a parking garage. On the first floor, right next to the hotel door, are our already-known infinitely many infinite buses. But then we notice: the garage has infinitely many floors, each with infinitely many infinite buses. Can the Hilbert hotel deal with this added layer of infinity? The answer is yes! You can imagine using the previous method to make a single file of passengers on each floor of the parking garage, then tell each single file to go into one infinite bus. Now we have reduced the problem back to infinitely many infinite buses, which we know can be accommodated in the hotel.
What if we add another layer of infinity? For example, if there are infinitely many parking garages, each with infinitely many floors, each floor with infinitely many buses, each bus with infinitely many passengers? That’s four layers of infinity, and the answer is still yes! In fact, the answer is yes even for four thousand layers of infinity. Does it ever stop? Does Hilbert’s hotel ever fail to accommodate new guests? Is there an infinity that is too large for Hilbert’s hotel?
Yes, there is. Indeed, if we had infinitely many layers of infinity, all those people could not possibly be accommodated in Hilbert’s hotel. So ...what is happening? It turns out that all the infinities described, up to this last one, are of the same size. That size is called ℵ0 (aleph nought), the size of the set ℕ = {1, 2, 3, 4, . . .} and how many rooms there are at Hilbert’s hotel. It was Georg Cantor who in 1874 introduced the idea of how to compare the sizes of infinities, and showed that there exist infinities of different sizes. Several important mathematicians (Poincaré, Kronecker, and later Weyl) strongly opposed his ideas, as did some theologians—these claimed that Cantor’s ideas challenged the uniqueness of the absolute infinity of God. Hilbert, on the other hand, supported and defended Cantor.
Comparing sizes of infinite sets is not so different from comparing sizes of finite sets: to know if there are more chairs or more people in a lecture room, you do not have to count people and chairs and compare the two numbers. You can just glance at the room and see if there are empty chairs (more chairs than people) or people left standing up (more people than chairs): if every single person is seated in a chair and there are no empty chairs, then the set of the chairs and the set of people are of the same size. Similarly, if every passenger on the buses gets assigned a room in Hilbert’s hotel and no room is left empty, then the set of passengers is an infinity of the same size as the set of rooms in Hilbert’s hotel, ℵ0. Cantor used this idea to show that the set of real numbers, ℝ, is strictly larger than the set of natural numbers, ℕ; his beautiful argument became known as “Cantor’s diagonal.” Cantor also conjectured—and tried to prove but failed—the Continuum Hypothesis: that there is no infinite set strictly larger than ℕ but strictly smaller than ℝ. Hilbert included proving that that statement is true or false as the first problem on the famous list of twenty-three problems he presented at the 1900 International Congress of Mathematicians in Paris, which would shape the direction of mathematics research for decades to come. The answer is that this hypothesis cannot be proved to be false (Gödel, 1940s) but it also cannot be proved to be true (Cohen, 1960s): it is an undecidable problem!
Hilbert famously said, about Cantor’s ideas about infinity and all the new mathematics that they brought about: “No one shall expel us from the paradise that Cantor has created.”