Finding Structure in Big Data

How do we navigate the vast amount of data at our disposal? How do we choose a movie to watch, out of the 75,000 movies available on Netflix? Or a new book to read, among the 800,000 listed on Amazon? Or which news articles to read, out of the thousands written everyday? Increasingly, these tasks are being delegated to computers—​recommendation systems analyze a large amount of data on user behavior, and use what they learn to make personalized recommendations for each one of us.

In fact, you probably encounter recommendation systems on an everyday basis: from Netflix to Amazon to Google News, better recommendation systems translate to a better user experience. There are some basic questions we should ask: How good are these recommendations? In fact, a more basic question: What does “good” mean? And how do they do it? As we will see, there are a number of interesting mathematical questions at the heart of these issues—most importantly, there are many widely used algorithms (in practice) whose behavior we cannot explain. Why do these algorithms work so well? Obviously, we would like to put these algorithms on a rigorous theoretical foundation and understand the computational complexity of the problems they are trying to solve.

Here, I will focus on one running example and use this to explain the basic problems in detail, and some of the mathematical abstractions. Consider the case of Amazon. I have purchased some items on Amazon recently: a fancy set of cutting knives and a top-of-the-line skillet. What other products might I be interested in? The basic tenet of designing a recommendation system is that the more data you have available, the better your recommendations will be. For example, Amazon could search through its vast collection of user data for another customer (Alex) who has purchased the same two items. We both bought knives and a skillet, and Amazon can deduce that we have a common interest in cooking. The key is: perhaps Alex has bought another item, say a collection of cooking spices, and this is a good item to recommend to me, because I am also interested in cooking. So the message is: lots of data (about similar customers) helps!

Of course, Amazon’s job is not so easy. I also bought a Kindle. And what if someone else (Jeff) also bought a Kindle? I buy math books online, but maybe Jeff is more of a Harry Potter aficionado. Just because we both bought the same item (a Kindle) does not mean that you should recommend Harry Potter books to me, and you certainly would not want to recommend math books to Jeff! The key is: What do the items I have purchased tell Amazon about my interests? Ideally, similar customers help us identify similar products, and vice-versa.

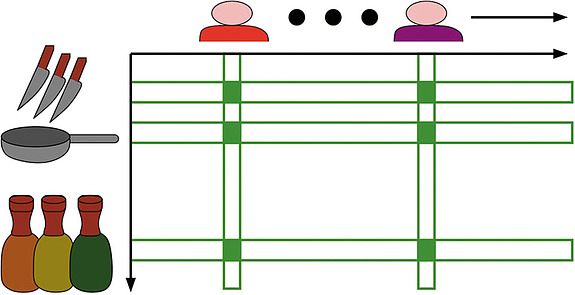
So how do they do it? Typically, the first step is to form a big table—rows represent items and columns represent users. And an entry indicates if a customer bought the corresponding item. What is the structure in this data? This is ultimately what we hope to use to make good recommendations. The basic idea is that a common interest is defined by a set of users (who share this interest) and a set of items. And we expect each customer to have bought many items in the set. We will call this a combinatorial rectangle (see image). The basic hypothesis is that the entire table of data we observe can be “explained” as a small number of these rectangles. So in this table containing information about millions of items and millions of users, we hope to “explain” the behavior of the users by a small number of rectangles—each representing a common interest.

The fundamental mathematical problem is: If the data can be “explained” by a small number of rectangles, can we find them? This problem is called nonnegative matrix factorization, and it plays a large role in the design of real recommendation systems.¹ In fact, there are many algorithms that work quite well in practice (on real data). But is there an efficient algorithm that provably works on every input? Recently, we showed that the answer is yes!²

Our algorithm is based on a connection to a purely algebraic question: Starting with the foundational work of Alfred Tarski and Abraham Seidenberg, a long line of research has focused on the task of deciding if a system of polynomial inequalities has a solution. This problem can be solved efficiently provided the number of distinct variables is small.³ And indeed, whether or not our table of data has a “good” nonnegative matrix factorization can be rephrased equivalently as whether or not a certain system of polynomial inequalities has a solution. So if our goal is to design fast algorithms, the operative question is: Can we reduce the number of variables? This is precisely the route we took, and it led us to a (much faster) provable algorithm for nonnegative matrix factorization whose running time is optimal under standard complexity assumptions.

Another fundamental mathematical question is: Can we give a theoretical explanation for why heuristics for these problems work so well in practice? There must be some property of the problems that we actually want to solve that makes them easier. In another work, we found a condition, which has been suggested within the machine learning community, that makes these problems much easier than in the worst case.⁴ The crux of the assumption is that for every “interest,” there must be some item that (if you buy it) is a strong indicator of your interest. For example, whoever buys a top-of-the-line skillet is probably interested in cooking. This assumption is known in the machine-learning literature as separability.⁵ In many instances of real data, practitioners have observed that this condition is met by the parameters that their algorithm finds. And what we showed is that under this condition, there are simple, fast algorithms that provably compute a nonnegative matrix factorization.

In fact, this is just one instance of a broader agenda: I believe that exploring these types of questions will be an important step in building bridges between theory and practice. Our goal should not be to find a theoretical framework in which recommendations (and learning, more generally) are computationally hard problems, but rather one in which learning is easy—one that explains (for example) why simple recommendation systems are so good. These questions lie somewhere between statistics and computer science, because the question is not: How much data do you need to make good recommendations (e.g., the statistical efficiency of an estimator)? Algorithms that use the bare minimum amount of data are all too often very hard to compute. The emerging question is: What are the best tradeoffs between making the most of your data, and running in some reasonable amount of time? The mathematical challenges abound in bringing these perspectives into not just recommendation systems—but into machine learning in general.